Next: Probability Interpretation of Wavefunction Up: Wave Mechanics Previous: Representation of Waves via Contents
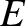 and linear momentum
and linear momentum  , moving in the
, moving in the  -direction (say),
can be represented by a one-dimensional complex wavefunction of the form
where the complex amplitude,
-direction (say),
can be represented by a one-dimensional complex wavefunction of the form
where the complex amplitude,  , is arbitrary, while the wavenumber,
, is arbitrary, while the wavenumber,  , and the angular frequency,
, and the angular frequency,  ,
are related to the particle momentum,
,
are related to the particle momentum,  , and energy,
, and energy, 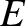 , via the fundamental
relations (11.3) and (11.1), respectively. The previous one-dimensional wavefunction is the solution of
a one-dimensional wave equation that determines how the wavefunction evolves in time.
As described below, we can guess the form of this wave equation by drawing an analogy with classical physics.
, via the fundamental
relations (11.3) and (11.1), respectively. The previous one-dimensional wavefunction is the solution of
a one-dimensional wave equation that determines how the wavefunction evolves in time.
As described below, we can guess the form of this wave equation by drawing an analogy with classical physics.
A classical particle of mass 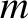 , moving in a one-dimensional potential
, moving in a one-dimensional potential 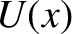 , satisfies the energy conservation
equation
, satisfies the energy conservation
equation
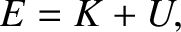 |
(11.16) |
 |
(11.17) |
However, it follows from Equations (11.1) and (11.15) that
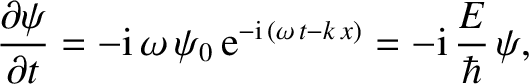 |
(11.19) |
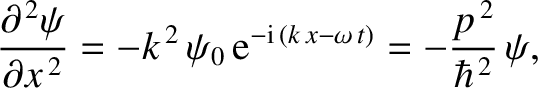 |
(11.21) |
For a massive particle moving in free space (i.e., 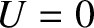 ), the complex wavefunction (11.15) is a
solution of Schrödinger's equation, (11.23), provided
), the complex wavefunction (11.15) is a
solution of Schrödinger's equation, (11.23), provided
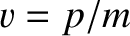 ,
of a massive (non-relativistic) particle.
,
of a massive (non-relativistic) particle.