- 9.1
- We can reproduce Equation (7.194)
by realizing that
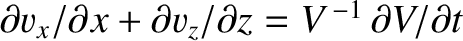 , where
, where 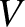 is the
volume of a small co-moving volume element. Combining this expression with the definition of bulk modulus,
is the
volume of a small co-moving volume element. Combining this expression with the definition of bulk modulus,
 , we obtain
, we obtain
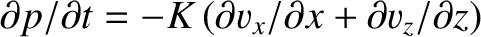 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 9.2
- Taking the finite compressibility of water into account,
this equation generalizes to
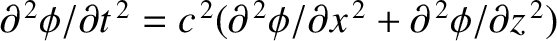 , where
, where
 is the velocity of sound. However, the left-hand side of the general equation is negligible for gravity waves, whose propagation velocities are much less than
is the velocity of sound. However, the left-hand side of the general equation is negligible for gravity waves, whose propagation velocities are much less than
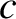 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 11.1
- Plural of quantum: Latin neuter
of quantus: how much?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
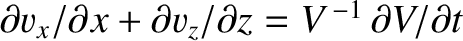 , where
, where 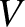 is the
volume of a small co-moving volume element. Combining this expression with the definition of bulk modulus,
is the
volume of a small co-moving volume element. Combining this expression with the definition of bulk modulus,
 , we obtain
, we obtain
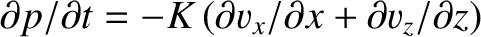 .
.
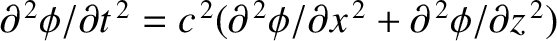 , where
, where
 is the velocity of sound. However, the left-hand side of the general equation is negligible for gravity waves, whose propagation velocities are much less than
is the velocity of sound. However, the left-hand side of the general equation is negligible for gravity waves, whose propagation velocities are much less than
 .
.