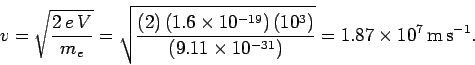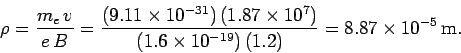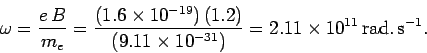Next: Example 8.3: Ampère's circuital
Up: Magnetism
Previous: Example 8.1: Earth's magnetic
Question: Suppose that an electron is accelerated from
rest through a voltage
difference of 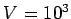 volts and then passes into a region containing a uniform
magnetic field of magnitude
volts and then passes into a region containing a uniform
magnetic field of magnitude 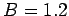 T. The electron subsequently executes a
closed circular
orbit in the plane perpendicular to the field. What is the radius of this
orbit? What is the angular frequency of gyration of the electron?
T. The electron subsequently executes a
closed circular
orbit in the plane perpendicular to the field. What is the radius of this
orbit? What is the angular frequency of gyration of the electron?
Answer: If an electron of mass
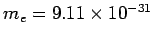 kg and charge
kg and charge
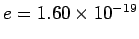 C is accelerated
from rest through a potential difference
C is accelerated
from rest through a potential difference  then its final
kinetic energy is
then its final
kinetic energy is
Thus, the final velocity  of the electron is given by
of the electron is given by
The initial direction of motion of the electron is at right-angles
to the direction of the magnetic field, otherwise the orbit of the electron
would be a spiral instead of a closed circle. Thus, we can use Eq. (167)
to calculate the radius 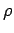 of the orbit. We obtain
of the orbit. We obtain
The angular frequency of gyration 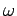 of the electron comes from Eq. (168):
of the electron comes from Eq. (168):



Next: Example 8.3: Ampère's circuital
Up: Magnetism
Previous: Example 8.1: Earth's magnetic
Richard Fitzpatrick
2007-07-14