


Next: Surface Integrals
Up: Vectors
Previous: Vector Calculus
A vector field is defined as a set of vectors associated with each point in space.
For instance, the velocity
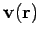 in a moving liquid
(e.g., a whirlpool) constitutes
a vector field. By analogy, a scalar field is a set of scalars associated with each
point in space. An example of a scalar field is the temperature distribution
in a moving liquid
(e.g., a whirlpool) constitutes
a vector field. By analogy, a scalar field is a set of scalars associated with each
point in space. An example of a scalar field is the temperature distribution 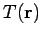 in
a furnace.
in
a furnace.
Consider a general vector field
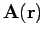 . Line integrals of the form
. Line integrals of the form
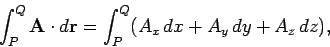 |
(44) |
evaluated on some particular path taken between two fixed points 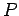 and
and 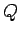 ,
often arise in Physics. Here
,
often arise in Physics. Here
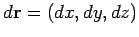 is
a path element. The path
might be specified as
is
a path element. The path
might be specified as 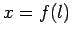 ,
, 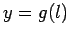 , and
, and 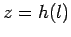 , where
, where
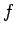 ,
, 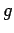 ,
, 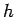 are mathematical functions, and
are mathematical functions, and 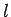 is a parameter (such as path-length) which varies monotonically
along the path. It follows that
is a parameter (such as path-length) which varies monotonically
along the path. It follows that
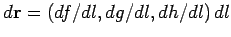 .
In particular, if
.
In particular, if
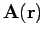 is a force-field then the line integral is the work done by the force in going between points
is a force-field then the line integral is the work done by the force in going between points
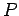 and
and 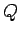 along the given path [cf., Eq. (26)].
Finally, if the path is a closed loop (i.e., if
along the given path [cf., Eq. (26)].
Finally, if the path is a closed loop (i.e., if 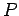 and
and 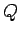 are the same point) then the integral is conventionally written
are the same point) then the integral is conventionally written
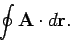 |
(45) |
As an example of a path integral, consider the work done in a repulsive, inverse-square,
central field,
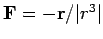 . The
element of work done is
. The
element of work done is
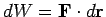 .
Take
.
Take
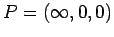 and
and 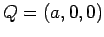 . Route 1 is along the
. Route 1 is along the  -axis, so
-axis, so
![\begin{displaymath}
W = \int_{\infty}^a \left(-\frac{1}{x^2}\right)\,dx = \left[\frac{1}{x}\right]_{\infty}^a
=\frac{1}{a}.
\end{displaymath}](img192.png) |
(46) |
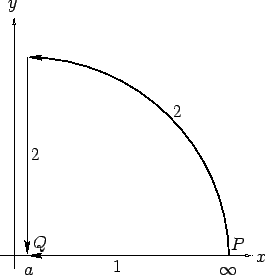
The second route is, firstly, around a large circle (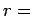 constant) to the point
(
constant) to the point
(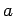 ,
, 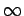 , 0), and then parallel to the
, 0), and then parallel to the 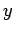 -axis--see Fig. 8. In the first, part no work is
done,
since
-axis--see Fig. 8. In the first, part no work is
done,
since 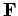 is perpendicular to
is perpendicular to 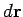 . In the second part,
. In the second part,
![\begin{displaymath}
W = \int_{\infty}^0 \frac{-y\,dy}{(a^2 + y^2)^{3/2}} = \left[\frac{1}{(y^2+a^2)^{1/2}}
\right]^0_\infty = \frac{1}{a}.
\end{displaymath}](img196.png) |
(47) |
In this case, the integral is independent of the path taken between the beginning and end points. However, not all line integrals
are path independent. Indeed, there are two different classes of
line integral--those whose values only depend on the end points, and
those whose values depend both on the end points and the path taken
between these points.
Figure 8:
An example line integral.
 |



Next: Surface Integrals
Up: Vectors
Previous: Vector Calculus
Richard Fitzpatrick
2007-07-14
![]() . Line integrals of the form
. Line integrals of the form
![]() . The
element of work done is
. The
element of work done is
![]() .
Take
.
Take
![]() and
and ![]() . Route 1 is along the
. Route 1 is along the ![]() -axis, so
-axis, so
![\begin{displaymath}
W = \int_{\infty}^0 \frac{-y\,dy}{(a^2 + y^2)^{3/2}} = \left[\frac{1}{(y^2+a^2)^{1/2}}
\right]^0_\infty = \frac{1}{a}.
\end{displaymath}](img196.png)