


Next: Line Integrals
Up: Vectors
Previous: The Vector Product
Suppose that vector 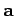 varies with time, so that
varies with time, so that
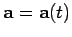 . The time
derivative of the vector is defined
. The time
derivative of the vector is defined
![\begin{displaymath}
\frac{d {\bf a}}{dt} = \lim_{\delta t\rightarrow 0} \left[\frac{{\bf a}(t+\delta t) - {\bf a}(t)}
{\delta t}\right].
\end{displaymath}](img165.png) |
(38) |
When written out in component form this becomes
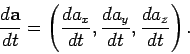 |
(39) |
Suppose that 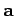 is, in fact, the product of a scalar
is, in fact, the product of a scalar 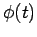 and another vector
and another vector
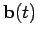 . What now is the time derivative of
. What now is the time derivative of 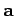 ? We have
? We have
 |
(40) |
which implies that
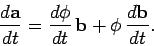 |
(41) |
It is easily demonstrated that
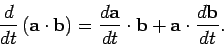 |
(42) |
Likewise,
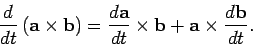 |
(43) |
It can be seen that the laws of vector differentiation are fairly analogous to those in
conventional calculus.



Next: Line Integrals
Up: Vectors
Previous: The Vector Product
Richard Fitzpatrick
2007-07-14
![\begin{displaymath}
\frac{d {\bf a}}{dt} = \lim_{\delta t\rightarrow 0} \left[\frac{{\bf a}(t+\delta t) - {\bf a}(t)}
{\delta t}\right].
\end{displaymath}](img165.png)
![\begin{displaymath}
\frac{d {\bf a}}{dt} = \lim_{\delta t\rightarrow 0} \left[\frac{{\bf a}(t+\delta t) - {\bf a}(t)}
{\delta t}\right].
\end{displaymath}](img165.png)
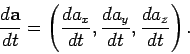
![]() is, in fact, the product of a scalar
is, in fact, the product of a scalar ![]() and another vector
and another vector
![]() . What now is the time derivative of
. What now is the time derivative of ![]() ? We have
? We have