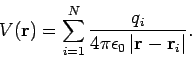Next: Worked Examples
Up: Electric Potential
Previous: Electric Potential and Electric
Let us calculate the electric potential 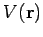 generated by a point charge
generated by a point charge 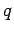 located at
the origin. It is fairly obvious, by symmetry, and also by looking at Fig. 14, that
located at
the origin. It is fairly obvious, by symmetry, and also by looking at Fig. 14, that
 is a
function of
is a
function of 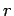 only, where
only, where 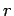 is the radial distance
from the origin. Thus, without loss of generality, we can restrict our
investigation to the
potential
is the radial distance
from the origin. Thus, without loss of generality, we can restrict our
investigation to the
potential  generated along the positive
generated along the positive 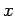 -axis. The
-axis. The 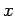 -component of the electric
field generated along this axis takes the form
-component of the electric
field generated along this axis takes the form
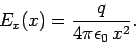 |
(94) |
Both the
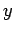 - and
- and 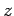 -components of the field are zero. According to Eq. (87),
-components of the field are zero. According to Eq. (87), 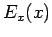 and
and
 are related via
are related via
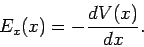 |
(95) |
Thus, by integration,
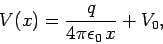 |
(96) |
where 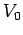 is an arbitrary constant. Finally, making use of the
fact that
is an arbitrary constant. Finally, making use of the
fact that 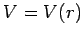 , we obtain
, we obtain
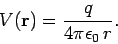 |
(97) |
Here, we have adopted the common convention that the potential at infinity
is zero. A potential defined according to this convention is called
an absolute potential.
Suppose that we have  point charges distributed in space. Let the
point charges distributed in space. Let the
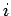 th charge
th charge 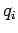 be located at position vector
be located at position vector 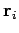 . Since
electric potential is superposable, and is also a scalar quantity, the
absolute potential at position vector
. Since
electric potential is superposable, and is also a scalar quantity, the
absolute potential at position vector 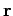 is simply the
algebraic sum of the potentials generated by each charge taken in
isolation:
is simply the
algebraic sum of the potentials generated by each charge taken in
isolation:
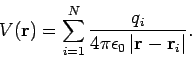 |
(98) |
The work 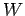 we would perform in taking a charge
we would perform in taking a charge 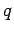 from infinity and slowly moving
it to point
from infinity and slowly moving
it to point 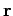 is the same as the increase in electric potential
energy of the charge during its journey [see Eq. (79)]. This,
by definition, is equal to the product of the charge
is the same as the increase in electric potential
energy of the charge during its journey [see Eq. (79)]. This,
by definition, is equal to the product of the charge 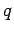 and the increase in
the electric potential. This, finally, is the same as
and the increase in
the electric potential. This, finally, is the same as 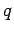 times the
absolute potential at point
times the
absolute potential at point 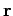 : i.e.,
: i.e.,
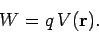 |
(99) |



Next: Worked Examples
Up: Electric Potential
Previous: Electric Potential and Electric
Richard Fitzpatrick
2007-07-14
![]() point charges distributed in space. Let the
point charges distributed in space. Let the
![]() th charge
th charge ![]() be located at position vector
be located at position vector ![]() . Since
electric potential is superposable, and is also a scalar quantity, the
absolute potential at position vector
. Since
electric potential is superposable, and is also a scalar quantity, the
absolute potential at position vector ![]() is simply the
algebraic sum of the potentials generated by each charge taken in
isolation:
is simply the
algebraic sum of the potentials generated by each charge taken in
isolation: