


Next: Electric Potential of a
Up: Electric Potential
Previous: Electric Potential
Electric Potential and Electric Field
We have seen that the difference in electric potential between two
arbitrary points in space is a function of the electric field which permeates space,
but is independent of the test charge used to measure this difference.
Let us investigate the relationship between electric potential and the electric
field.
Consider a charge 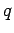 which is slowly moved an infinitesimal distance
which is slowly moved an infinitesimal distance 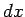 along the
along the  -axis. Suppose that the difference in electric potential
between the final and initial positions of the charge is
-axis. Suppose that the difference in electric potential
between the final and initial positions of the charge is 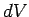 .
By definition, the change
.
By definition, the change 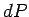 in the charge's electric potential energy
is given by
in the charge's electric potential energy
is given by
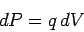 |
(84) |
From Eq. (76), the work 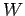 which we perform in moving the charge is
which we perform in moving the charge is
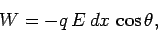 |
(85) |
where 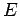 is the local electric field-strength, and
is the local electric field-strength, and 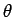 is the angle subtended
between the direction of the field and the
is the angle subtended
between the direction of the field and the  -axis. By definition,
-axis. By definition,
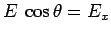 , where
, where 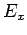 is the
is the  -component of the local electric field.
Energy conservation demands that
-component of the local electric field.
Energy conservation demands that
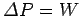 (i.e., the increase in the charge's energy matches the
work done on the charge), or
(i.e., the increase in the charge's energy matches the
work done on the charge), or
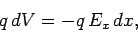 |
(86) |
which reduces to
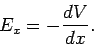 |
(87) |
We call the quantity 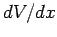 the gradient of the
electric potential in the
the gradient of the
electric potential in the  -direction. It basically measures how fast
the potential
-direction. It basically measures how fast
the potential 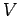 varies as the coordinate
varies as the coordinate  is changed (but the
coordinates
is changed (but the
coordinates 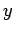 and
and 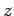 are held constant). Thus, the above formula is saying
that the
are held constant). Thus, the above formula is saying
that the  -component of the electric field at a given point in space is equal
to minus the local gradient of the electric potential in the
-component of the electric field at a given point in space is equal
to minus the local gradient of the electric potential in the
 -direction.
-direction.
According to Eq. (87), electric field strength has dimensions
of potential difference
over length. It follows that the units of electric field are volts
per meter (
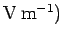 .
Of course, these new units are entirely equivalent to
newtons per coulomb: i.e.,
.
Of course, these new units are entirely equivalent to
newtons per coulomb: i.e.,
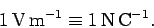 |
(88) |
Consider the special case of a uniform  -directed electric field
-directed electric field 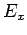 generated by two uniformly charged parallel planes normal to the
generated by two uniformly charged parallel planes normal to the  -axis. It is
clear, from Eq. (87), that if
-axis. It is
clear, from Eq. (87), that if 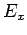 is to be constant between the plates
then
is to be constant between the plates
then 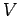 must vary linearly with
must vary linearly with  in this region. In fact, it is
easily shown that
in this region. In fact, it is
easily shown that
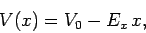 |
(89) |
where 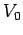 is an arbitrary constant. According to Eq. (89), the electric potential
is an arbitrary constant. According to Eq. (89), the electric potential 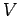 decreases
continuously as we move
along the direction of the electric field. Since a positive charge is
accelerated in this direction, we conclude that positive charges are
accelerated down gradients in the electric potential, in much the same manner
as masses fall down gradients of gravitational potential (which is, of course,
proportional to height). Likewise, negative charges are accelerated up
gradients in the electric potential.
decreases
continuously as we move
along the direction of the electric field. Since a positive charge is
accelerated in this direction, we conclude that positive charges are
accelerated down gradients in the electric potential, in much the same manner
as masses fall down gradients of gravitational potential (which is, of course,
proportional to height). Likewise, negative charges are accelerated up
gradients in the electric potential.
According to Eq. (87), the  -component of the electric field is equal
to minus the gradient of the electric potential in the
-component of the electric field is equal
to minus the gradient of the electric potential in the  -direction.
Since there is nothing special about the
-direction.
Since there is nothing special about the  -direction, analogous rules
must exist for the
-direction, analogous rules
must exist for the 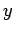 - and
- and 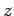 -components of the field.
These three rules can be combined to give
-components of the field.
These three rules can be combined to give
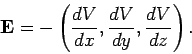 |
(90) |
Here, the  derivative is taken at constant
derivative is taken at constant 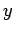 and
and 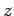 , etc.
The above expression shows how the electric field
, etc.
The above expression shows how the electric field
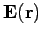 , which is a vector field, is related to the electric
potential
, which is a vector field, is related to the electric
potential 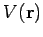 , which is a scalar field.
, which is a scalar field.
We have seen that electric fields are superposable. That is, the electric
field generated by a set of charges distributed in space is
simply the vector sum of the electric fields generated by each charge
taken separately. Well, if electric fields are superposable, it follows
from Eq. (90) that electric potentials must also be superposable. Thus,
the electric potential generated by a set of charges distributed in space
is just the scalar sum of the potentials generated by each charge taken in isolation. Clearly, it is far easier to determine the potential generated by a set
of charges than it is to determine the electric field, since we can
sum the potentials
generated by the individual charges algebraically, and do not have to worry about
their directions (since they have no directions).
Equation (90) looks rather forbidding. Fortunately, however, it is possible
to rewrite this equation in a more appealing form. Consider two neighboring
points 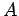 and
and 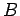 . Suppose that
. Suppose that
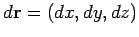 is the vector displacement of point
is the vector displacement of point 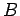 relative to point
relative to point 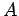 .
Let
.
Let 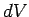 be the difference in electric potential
between these two points.
Suppose that we travel from
be the difference in electric potential
between these two points.
Suppose that we travel from 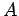 to
to 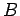 by first moving a distance
by first moving a distance 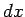 along the
along the  -axis, then moving
-axis, then moving 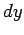 along the
along the 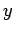 -axis,
and finally moving
-axis,
and finally moving 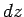 along the
along the 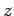 -axis. The net increase
in the electric potential
-axis. The net increase
in the electric potential 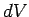 as we move from
as we move from 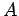 to
to 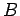 is simply the sum of the increases
is simply the sum of the increases 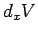 as we move along the
as we move along the  -axis,
-axis,
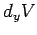 as we move along the
as we move along the 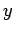 -axis, and
-axis, and 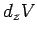 as we move along the
as we move along the 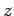 -axis:
-axis:
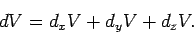 |
(91) |
But, according to Eq. (90),
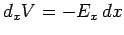 , etc.
So, we obtain
, etc.
So, we obtain
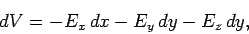 |
(92) |
which is equivalent to
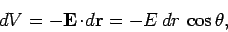 |
(93) |
where 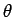 is the angle subtended between the vector
is the angle subtended between the vector 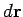 and
the local electric field
and
the local electric field 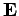 . Note that
. Note that 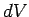 attains
its most negative value when
attains
its most negative value when 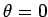 . In other words, the direction of the
electric field at point
. In other words, the direction of the
electric field at point 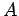 corresponds to the direction in which the electric
potential
corresponds to the direction in which the electric
potential 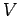 decreases most rapidly. A positive charge placed at point
decreases most rapidly. A positive charge placed at point 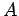 is accelerated in this direction. Likewise, a negative charge placed at
is accelerated in this direction. Likewise, a negative charge placed at 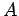 is
accelerated in the direction in which the potential increases most rapidly
(i.e.,
is
accelerated in the direction in which the potential increases most rapidly
(i.e.,
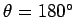 ). Suppose that we move from point
). Suppose that we move from point 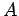 to a neighboring point
to a neighboring point
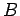 in a direction perpendicular to that of the local electric
field (i.e.,
in a direction perpendicular to that of the local electric
field (i.e.,
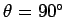 ). In this case, it follows from Eq. (93) that the points
). In this case, it follows from Eq. (93) that the points 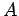 and
and 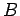 lie at the same electric potential (i.e.,
lie at the same electric potential (i.e., 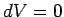 ). The locus of all the points in the vicinity of point
). The locus of all the points in the vicinity of point 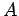 which lie at the
same potential as
which lie at the
same potential as 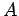 is a plane perpendicular to the direction of the
local electric
field. More generally, the surfaces of constant electric potential, the so-called
equipotential surfaces, exist as a set of non-interlocking surfaces which are
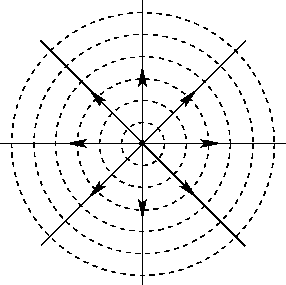
everywhere perpendicular to the direction of the electric field. Figure 14 shows the
equipotential surfaces (dashed lines) and electric field-lines (solid lines)
generated by a positive point charge. In this case, the equipotential surfaces are
spheres centred on the charge.
is a plane perpendicular to the direction of the
local electric
field. More generally, the surfaces of constant electric potential, the so-called
equipotential surfaces, exist as a set of non-interlocking surfaces which are
everywhere perpendicular to the direction of the electric field. Figure 14 shows the
equipotential surfaces (dashed lines) and electric field-lines (solid lines)
generated by a positive point charge. In this case, the equipotential surfaces are
spheres centred on the charge.
Figure 14:
The equipotential surfaces (dashed lines) and the electric
field-lines (solid lines) of a positive point charge.
 |
In Sect. 4.3, we found that the electric field immediately above the surface of
a conductor is directed perpendicular to that surface. Thus, it is clear that the
surface of a conductor must correspond to an equipotential surface. In fact, since there
is no electric field inside a conductor (and, hence, no gradient in the electric
potential), it follows that the whole conductor (i.e., both the surface and the
interior) lies at the same electric potential.



Next: Electric Potential of a
Up: Electric Potential
Previous: Electric Potential
Richard Fitzpatrick
2007-07-14
![]() which is slowly moved an infinitesimal distance
which is slowly moved an infinitesimal distance ![]() along the
along the ![]() -axis. Suppose that the difference in electric potential
between the final and initial positions of the charge is
-axis. Suppose that the difference in electric potential
between the final and initial positions of the charge is ![]() .
By definition, the change
.
By definition, the change ![]() in the charge's electric potential energy
is given by
in the charge's electric potential energy
is given by
![]() .
Of course, these new units are entirely equivalent to
newtons per coulomb: i.e.,
.
Of course, these new units are entirely equivalent to
newtons per coulomb: i.e.,
![]() -directed electric field
-directed electric field ![]() generated by two uniformly charged parallel planes normal to the
generated by two uniformly charged parallel planes normal to the ![]() -axis. It is
clear, from Eq. (87), that if
-axis. It is
clear, from Eq. (87), that if ![]() is to be constant between the plates
then
is to be constant between the plates
then ![]() must vary linearly with
must vary linearly with ![]() in this region. In fact, it is
easily shown that
in this region. In fact, it is
easily shown that
![]() -component of the electric field is equal
to minus the gradient of the electric potential in the
-component of the electric field is equal
to minus the gradient of the electric potential in the ![]() -direction.
Since there is nothing special about the
-direction.
Since there is nothing special about the ![]() -direction, analogous rules
must exist for the
-direction, analogous rules
must exist for the ![]() - and
- and ![]() -components of the field.
These three rules can be combined to give
-components of the field.
These three rules can be combined to give
![]() and
and ![]() . Suppose that
. Suppose that
![]() is the vector displacement of point
is the vector displacement of point ![]() relative to point
relative to point ![]() .
Let
.
Let ![]() be the difference in electric potential
between these two points.
Suppose that we travel from
be the difference in electric potential
between these two points.
Suppose that we travel from ![]() to
to ![]() by first moving a distance
by first moving a distance ![]() along the
along the ![]() -axis, then moving
-axis, then moving ![]() along the
along the ![]() -axis,
and finally moving
-axis,
and finally moving ![]() along the
along the ![]() -axis. The net increase
in the electric potential
-axis. The net increase
in the electric potential ![]() as we move from
as we move from ![]() to
to ![]() is simply the sum of the increases
is simply the sum of the increases ![]() as we move along the
as we move along the ![]() -axis,
-axis,
![]() as we move along the
as we move along the ![]() -axis, and
-axis, and ![]() as we move along the
as we move along the ![]() -axis:
-axis:
