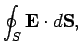 |
(319) | ||
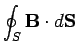 |
(320) | ||
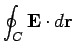 |
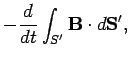 |
(321) | |
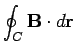 |
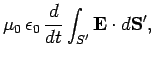 |
(322) |
Maxwell was primarily interested in electromagnetic
waves which can propagate through a vacuum (i.e.,
a region containing no charges or currents).
Now, in a vacuum, Maxwell's equations
reduce to
Consider a plane electromagnetic wave propagating along the
![]() -axis. According to Maxwell's calculations, the electric and
magnetic fields associated with such a wave take the form
-axis. According to Maxwell's calculations, the electric and
magnetic fields associated with such a wave take the form
| (326) |
Maxwell was able to establish that electromagnetic waves possess the following properties:
| (327) |
According to Eqs. (321) and (322), a changing magnetic field generates an electric field, and a changing electric field generates a magnetic field. Thus, we can think of the propagation of an electromagnetic field through a vacuum as due to a kind of ``leap-frog'' effect, in which a changing electric field generates a magnetic field, which, in turn, generates an electric field, and so on. Note that the displacement current term in Eq. (322) plays a crucial role in the propagation of electromagnetic waves. Indeed, without this term, a changing electric field is incapable of generating a magnetic field, and so there can be no leap-frog effect. Electromagnetic waves have many properties in common with other types of wave (e.g., sound waves). However, they are unique in one respect: i.e., they are able to propagate through a vacuum. All other types of waves require some sort of medium through which to propagate.
Maxwell deduced that the speed of propagation of an electromagnetic
wave through a vacuum is entirely
determined by the constants ![]() and
and ![]() [see Eq. (328)]. The former constant is related to the strength of the
magnetic field generated by a steady current, whereas the latter constant
is related to the strength of the electric field generated by a stationary
charge. The values of both constants
were well known in Maxwell's day. In modern units,
[see Eq. (328)]. The former constant is related to the strength of the
magnetic field generated by a steady current, whereas the latter constant
is related to the strength of the electric field generated by a stationary
charge. The values of both constants
were well known in Maxwell's day. In modern units,
![]() and
and
![]() .
Thus, when Maxwell calculated the velocity of electromagnetic waves he obtained
.
Thus, when Maxwell calculated the velocity of electromagnetic waves he obtained
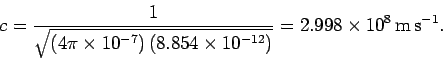 |
(329) |
Maxwell was able to make another remarkable prediction. The wavelength of
light was well known in the late nineteenth century from studies of diffraction
through slits, etc.
Visible light actually occupies a surprisingly
narrow range of wavelengths. The shortest wavelength blue light which is visible
has a wavelength of ![]() microns (one micron is
microns (one micron is ![]() meters).
The longest wavelength red light which is visible has a wavelength of
meters).
The longest wavelength red light which is visible has a wavelength of
![]() microns. However, there is nothing in Maxwell's
analysis which suggested that
this particular range of wavelengths is special.
In principle, electromagnetic waves
can have any wavelength.
Maxwell concluded that visible light forms
a small element of a vast spectrum of
previously undiscovered
types of electromagnetic radiation.
microns. However, there is nothing in Maxwell's
analysis which suggested that
this particular range of wavelengths is special.
In principle, electromagnetic waves
can have any wavelength.
Maxwell concluded that visible light forms
a small element of a vast spectrum of
previously undiscovered
types of electromagnetic radiation.
Since Maxwell's time, virtually all of the
non-visible parts of the electromagnetic spectrum have been observed.
Table 3 gives a brief guide to the electromagnetic spectrum.
Electromagnetic waves are of particular importance because they
are our only source of information regarding the Universe around us.
Radio waves and microwaves (which are comparatively
hard to scatter) have provided much of
our knowledge about the centre of the Galaxy. This is completely unobservable
in visible light, which is strongly scattered by interstellar gas and dust
lying in the galactic plane.
For the same reason, the spiral arms of the Galaxy can only be mapped out using radio waves.
Infrared radiation is useful for detecting
proto-stars which are not yet hot enough to emit visible radiation.
Of course, visible radiation is still the mainstay of astronomy.
Satellite based ultraviolet observations have yielded invaluable insights into
the structure and distribution of distant galaxies. Finally, X-ray and ![]() -ray
astronomy usually concentrates on exotic objects in the Galaxy such as pulsars
and supernova remnants.
-ray
astronomy usually concentrates on exotic objects in the Galaxy such as pulsars
and supernova remnants.