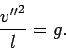Next: Rotational motion
Up: Circular motion
Previous: Worked example 7.4: Aerobatic
Question: A bullet of mass 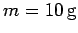 strikes a pendulum bob
of mass
strikes a pendulum bob
of mass
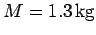 horizontally with speed
horizontally with speed  , and then becomes embedded in the bob. The bob
is initially at rest, and is suspended by a stiff rod of length
, and then becomes embedded in the bob. The bob
is initially at rest, and is suspended by a stiff rod of length
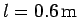 and negligible mass. The bob is free to rotate in the vertical direction.
What is the minimum value of
and negligible mass. The bob is free to rotate in the vertical direction.
What is the minimum value of  which causes the bob to execute a
complete vertical circle? How does the answer change if the bob is suspended from
a light flexible rod (of the same length), instead of a stiff rod?
which causes the bob to execute a
complete vertical circle? How does the answer change if the bob is suspended from
a light flexible rod (of the same length), instead of a stiff rod?
Answer: When the bullet strikes the bob, and then sticks to it, the bullet and
bob move off with a velocity 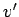 which is given by momentum conservation:
which is given by momentum conservation:
Hence,
Consider the case where the bob is suspended by a rigid rod.
If the bob and bullet only just manage to execute a vertical loop, then their initial kinetic
energy
 must only just be sufficient to lift them from the bottom
to the top of the loop--a distance
must only just be sufficient to lift them from the bottom
to the top of the loop--a distance 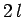 . Hence, in this critical case,
energy conservation yields
. Hence, in this critical case,
energy conservation yields
which implies
or
Consider the case where the bob is suspended by a flexible rod.
The velocity 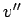 of the bob and bullet at the top of the loop is obtained from energy
conservation:
of the bob and bullet at the top of the loop is obtained from energy
conservation:
If the bob and bullet only just manage to execute a vertical loop, then the tension
in the rod is zero at the top of the loop. Hence, the acceleration due to
gravity 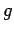 must account exactly for the required acceleration
must account exactly for the required acceleration 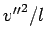 towards the centre of the loop:
towards the centre of the loop:
It follows that, in this critical case,
or



Next: Rotational motion
Up: Circular motion
Previous: Worked example 7.4: Aerobatic
Richard Fitzpatrick
2006-02-02
![]() which is given by momentum conservation:
which is given by momentum conservation:
![]() must only just be sufficient to lift them from the bottom
to the top of the loop--a distance
must only just be sufficient to lift them from the bottom
to the top of the loop--a distance ![]() . Hence, in this critical case,
energy conservation yields
. Hence, in this critical case,
energy conservation yields
![]() of the bob and bullet at the top of the loop is obtained from energy
conservation:
of the bob and bullet at the top of the loop is obtained from energy
conservation: