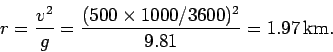

Question: A stunt pilot experiences weightlessness
momentarily at the top of a ``loop the loop'' maneuver. Given that the
speed of the stunt plane is
![]() , what is the radius
, what is the radius ![]() of the
loop?
of the
loop?
Answer: Let ![]() be the mass of the pilot.
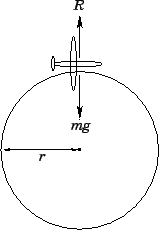
Consider the radial acceleration of the pilot at the
top of the loop. The pilot is subject to two radial forces: the gravitational
force
be the mass of the pilot.
Consider the radial acceleration of the pilot at the
top of the loop. The pilot is subject to two radial forces: the gravitational
force ![]() , which acts towards the centre of the loop, and the reaction force
, which acts towards the centre of the loop, and the reaction force ![]() ,
due to the plane, which acts away from the centre of the loop. Since the pilot
experiences an acceleration
,
due to the plane, which acts away from the centre of the loop. Since the pilot
experiences an acceleration ![]() towards the centre of the loop, Newton's second
law of motion yields
towards the centre of the loop, Newton's second
law of motion yields