


Next: Worked example 7.3: Amusement
Up: Circular motion
Previous: Worked example 7.1: A
Question: A car of mass
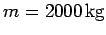 travels around a flat
circular race track of radius
travels around a flat
circular race track of radius
 . The car starts at rest, and its
speed increases at the constant rate
. The car starts at rest, and its
speed increases at the constant rate
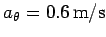 . What is the speed
of the car at the point when its centripetal and tangential accelerations are equal?
. What is the speed
of the car at the point when its centripetal and tangential accelerations are equal?
Answer: The tangential acceleration of the car is
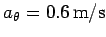 .
When the car travels with tangential velocity
.
When the car travels with tangential velocity  its centripetal acceleration is
its centripetal acceleration is
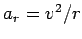 . Hence,
. Hence,
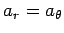 when
when
or
Richard Fitzpatrick
2006-02-02
![]() .
When the car travels with tangential velocity
.
When the car travels with tangential velocity ![]() its centripetal acceleration is
its centripetal acceleration is
![]() . Hence,
. Hence,
![]() when
when