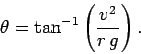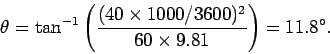Next: Worked example 7.2: Circular
Up: Circular motion
Previous: Motion on curved surfaces
Question: Civil engineers generally bank curves on roads in such a manner
that a car going around the curve at the recommended speed does not have to
rely on friction between its tires and the road surface in order to round the curve.
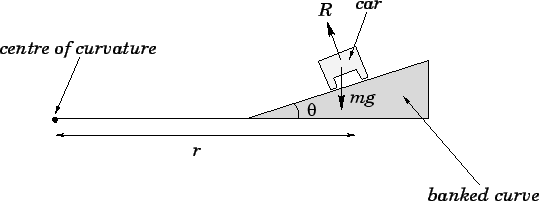
Suppose that the radius of curvature of a given curve is 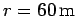 , and that
the recommended speed is
, and that
the recommended speed is
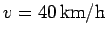 . At what angle
. At what angle  should the
curve be banked?
should the
curve be banked?
Answer: Consider a car of mass  going around the curve. The car's
weight,
going around the curve. The car's
weight,  , acts vertically downwards. The road surface exerts an upward normal reaction
, acts vertically downwards. The road surface exerts an upward normal reaction  on the car.
The vertical component of the reaction must balance the downward weight of the car, so
on the car.
The vertical component of the reaction must balance the downward weight of the car, so
The horizontal component of the reaction, 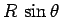 , acts towards the centre of curvature of
the road. This
component provides the force
, acts towards the centre of curvature of
the road. This
component provides the force  towards the centre of the curvature which the
car experiences as it rounds the curve. In other words,
towards the centre of the curvature which the
car experiences as it rounds the curve. In other words,
which yields
or
Hence,
Note that if the car attempts to round the curve at the wrong speed then
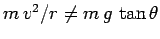 , and the difference has to be made up by a
sideways friction force exerted between the car's tires and the road surface. Unfortunately,
this does not always work--especially if the road surface is wet!
, and the difference has to be made up by a
sideways friction force exerted between the car's tires and the road surface. Unfortunately,
this does not always work--especially if the road surface is wet!



Next: Worked example 7.2: Circular
Up: Circular motion
Previous: Motion on curved surfaces
Richard Fitzpatrick
2006-02-02

![]() going around the curve. The car's
weight,
going around the curve. The car's
weight, ![]() , acts vertically downwards. The road surface exerts an upward normal reaction
, acts vertically downwards. The road surface exerts an upward normal reaction ![]() on the car.
The vertical component of the reaction must balance the downward weight of the car, so
on the car.
The vertical component of the reaction must balance the downward weight of the car, so