Worked example 1.1: Conversion of units

Question: Farmer Jones has recently brought a 40 acre field and wishes to replace the fence surrounding it. Given that the field is square, what length of fencing (in meters) should Farmer Jones purchase? Incidentally, 1 acre equals 43,560 square feet.
 
Answer: If 1 acre equals 43,560 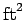${\rm ft}^2$ and 1 ft equals 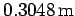$0.3048 {\rm m}$ (see Tab. 2) then

$$1 {\rm acre} = 43560 \times (0.3048)^2 = 4.047\times 10^3 {\rm m}^2.$$

Thus, the area of the field in mks units is

$$A = 40\times 4.047\times 10^3 = 1.619\times 10^5 {\rm m}^2.$$

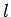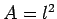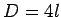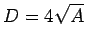Now, a square field with sides of length $l$ has an area $A=l^2$ and a circumference $D=4l$. Hence, $D=4\sqrt{A}$. It follows that the length of the fence is

$$D = 4\times \sqrt{1.619\times 10^5} = 1.609\times 10^3 {\rm m}.$$