


Next: Worked example 1.1: Conversion
Up: Introduction
Previous: Precision and significant figures
As we have already mentioned, length, mass, and time are three fundamentally different quantities
which are measured in three completely independent units. It, therefore, makes no sense for a
prospective law of physics to express an equality between (say) a length and a mass. In other
words, the example law
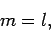 |
(3) |
where 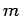 is a mass and
is a mass and 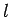 is a length, cannot possibly be correct. One easy way of
seeing that Eq. (3) is invalid (as a law of physics), is to note that this equation
is dependent on the adopted system of units: i.e., if
is a length, cannot possibly be correct. One easy way of
seeing that Eq. (3) is invalid (as a law of physics), is to note that this equation
is dependent on the adopted system of units: i.e., if 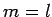 in mks units, then
in mks units, then
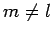 in fps units, because the conversion factors which must be
applied to the left- and right-hand
sides differ. Physicists hold very strongly to the assumption that the laws of physics
possess objective reality: in other words, the laws of physics are the same for
all observers. One immediate consequence of this assumption is that a law
of physics must take the same form in all possible systems of units that a prospective
observer might choose to employ. The only way in which this can be the case is if
all laws of physics are dimensionally consistent: i.e., the quantities
on the left- and right-hand sides of the equality sign in any given law of
physics must have the same dimensions (i.e.,
the same combinations of length, mass, and time). A dimensionally consistent equation
naturally takes the same form in all possible systems of units, since the same conversion
factors are applied to both sides of the equation when transforming from one system to another.
in fps units, because the conversion factors which must be
applied to the left- and right-hand
sides differ. Physicists hold very strongly to the assumption that the laws of physics
possess objective reality: in other words, the laws of physics are the same for
all observers. One immediate consequence of this assumption is that a law
of physics must take the same form in all possible systems of units that a prospective
observer might choose to employ. The only way in which this can be the case is if
all laws of physics are dimensionally consistent: i.e., the quantities
on the left- and right-hand sides of the equality sign in any given law of
physics must have the same dimensions (i.e.,
the same combinations of length, mass, and time). A dimensionally consistent equation
naturally takes the same form in all possible systems of units, since the same conversion
factors are applied to both sides of the equation when transforming from one system to another.
As an example, let us consider what is probably the most famous equation in physics:
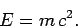 |
(4) |
Here, 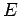 is the energy of a body,
is the energy of a body, 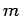 is its mass, and
is its mass, and 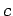 is the velocity of light in
vacuum. The dimensions of energy are
is the velocity of light in
vacuum. The dimensions of energy are
![$[M][L^2]/[T^2]$](img61.png) , and the dimensions of
velocity are
, and the dimensions of
velocity are ![$[L]/[T]$](img62.png) . Hence, the dimensions of the left-hand side are
. Hence, the dimensions of the left-hand side are
![$[M][L^2]/[T^2]$](img61.png) , whereas the dimensions of the right-hand side are
, whereas the dimensions of the right-hand side are
![$[M] ([L]/[T])^2= [M][L^2]/[T^2]$](img63.png) . It follows that Eq. (4) is indeed dimensionally
consistent. Thus,
. It follows that Eq. (4) is indeed dimensionally
consistent. Thus, 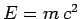 holds good in mks units, in cgs units, in fps units, and in
any other sensible
set of units. Had Einstein proposed
holds good in mks units, in cgs units, in fps units, and in
any other sensible
set of units. Had Einstein proposed 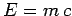 , or
, or 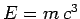 , then his error would
have been immediately apparent to other physicists, since these prospective laws
are not dimensionally consistent. In fact,
, then his error would
have been immediately apparent to other physicists, since these prospective laws
are not dimensionally consistent. In fact, 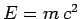 represents the only simple, dimensionally
consistent way of combining an energy, a mass, and the velocity of light in a law of
physics.
represents the only simple, dimensionally
consistent way of combining an energy, a mass, and the velocity of light in a law of
physics.
The last comment leads naturally to the subject of dimensional analysis: i.e.,
the use of the idea of dimensional consistency to guess the forms of simple laws of physics.
It should be noted that dimensional analysis is of fairly limited applicability, and
is a poor substitute for analysis employing the actual laws of physics; nevertheless,
it is occasionally useful. Suppose that a special effects studio wants to film a scene
in which the Leaning Tower of Pisa topples to the ground. In order to achieve this, the studio
might make a scale model of the tower, which is (say) 1m tall, and then film the model falling over.
The only problem is that the resulting footage would look completely unrealistic, because the model
tower would fall over too quickly. The studio could easily fix this problem by slowing the
film down. The question is by what factor should the film be slowed down in order to make it
look realistic?
Figure 1:
The Leaning Tower of Pisa
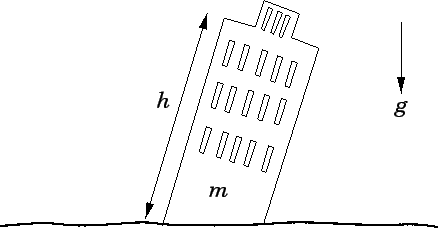 |
Although, at this stage, we do not know how to apply the laws of physics to the
problem of a tower falling over, we can, at least, make some educated guesses as to what factors
the time 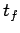 required for this process to occur depends on. In fact, it
seems reasonable to suppose that
required for this process to occur depends on. In fact, it
seems reasonable to suppose that 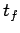 depends principally on the mass of the tower,
depends principally on the mass of the tower, 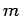 , the
height of the tower,
, the
height of the tower, 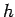 , and the acceleration due to gravity,
, and the acceleration due to gravity, 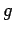 . See Fig. 1. In other words,
. See Fig. 1. In other words,
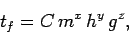 |
(5) |
where 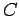 is a dimensionless constant, and
is a dimensionless constant, and  ,
, 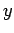 , and
, and 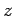 are unknown exponents. The
exponents
are unknown exponents. The
exponents  ,
, 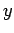 , and
, and 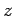 can be determined by the requirement that the above equation be dimensionally
consistent. Incidentally, the dimensions of an acceleration are
can be determined by the requirement that the above equation be dimensionally
consistent. Incidentally, the dimensions of an acceleration are ![$[L]/[T^2]$](img74.png) . Hence,
equating the dimensions of both sides of Eq. (5), we obtain
. Hence,
equating the dimensions of both sides of Eq. (5), we obtain
![\begin{displaymath}[T]= [M]^x [L]^y \left(\frac{[L]}{[T^2]}\right)^z.
\end{displaymath}](img75.png) |
(6) |
We can now compare the exponents of ![$[L]$](img76.png) ,
, ![$[M]$](img77.png) , and
, and ![$[T]$](img78.png) on either side of the
above expression: these exponents must all match in order for Eq. (5) to be dimensionally
consistent. Thus,
on either side of the
above expression: these exponents must all match in order for Eq. (5) to be dimensionally
consistent. Thus,
It immediately follows that 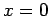 ,
, 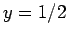 , and
, and 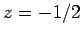 . Hence,
. Hence,
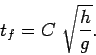 |
(10) |
Now, the actual tower of Pisa is approximately 100m tall. It follows that since
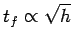 (
(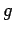 is the same for both the real and the model tower) then the
1m high model tower falls over a factor of
is the same for both the real and the model tower) then the
1m high model tower falls over a factor of
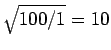 times faster than the real
tower. Thus, the film must be slowed down by a factor 10 in order to make it look realistic.
times faster than the real
tower. Thus, the film must be slowed down by a factor 10 in order to make it look realistic.



Next: Worked example 1.1: Conversion
Up: Introduction
Previous: Precision and significant figures
Richard Fitzpatrick
2006-02-02
![]() required for this process to occur depends on. In fact, it
seems reasonable to suppose that
required for this process to occur depends on. In fact, it
seems reasonable to suppose that ![]() depends principally on the mass of the tower,
depends principally on the mass of the tower, ![]() , the
height of the tower,
, the
height of the tower, ![]() , and the acceleration due to gravity,
, and the acceleration due to gravity, ![]() . See Fig. 1. In other words,
. See Fig. 1. In other words,
![\begin{displaymath}[T]= [M]^x [L]^y \left(\frac{[L]}{[T^2]}\right)^z.
\end{displaymath}](img75.png)
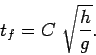
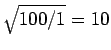 times faster than the real
tower. Thus, the film must be slowed down by a factor 10 in order to make it look realistic.
times faster than the real
tower. Thus, the film must be slowed down by a factor 10 in order to make it look realistic.