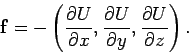Next: Motion in a general
Up: Conservation of energy
Previous: Potential energy
Hooke's law
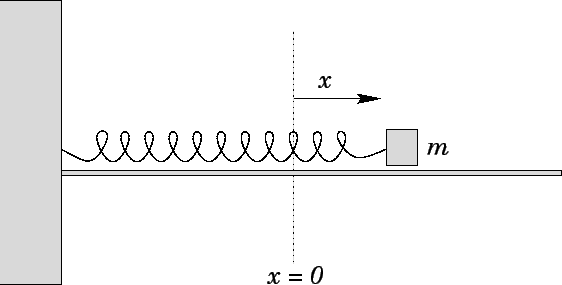
Consider a mass 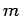 which slides over a horizontal frictionless surface. Suppose that
the mass is attached
to a light horizontal spring whose other end is anchored to an immovable object. See
Fig. 42. Let
which slides over a horizontal frictionless surface. Suppose that
the mass is attached
to a light horizontal spring whose other end is anchored to an immovable object. See
Fig. 42. Let  be the extension of the spring: i.e., the difference between
the spring's actual length and its unstretched length. Obviously,
be the extension of the spring: i.e., the difference between
the spring's actual length and its unstretched length. Obviously,  can also be used as
a coordinate to determine the horizontal displacement of the mass.
According to Hooke's law, the force
can also be used as
a coordinate to determine the horizontal displacement of the mass.
According to Hooke's law, the force
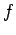 that the spring exerts on the mass is directly proportional to its extension, and always acts to reduce
this extension.
Hence, we can write
that the spring exerts on the mass is directly proportional to its extension, and always acts to reduce
this extension.
Hence, we can write
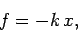 |
(159) |
where the positive quantity 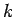 is called the force constant of the spring. Note that
the minus sign in the above equation ensures that the force always acts to reduce the
spring's extension:
e.g., if the extension is positive then the force acts to the left, so as to
shorten the spring.
is called the force constant of the spring. Note that
the minus sign in the above equation ensures that the force always acts to reduce the
spring's extension:
e.g., if the extension is positive then the force acts to the left, so as to
shorten the spring.
Figure 42:
Mass on a spring
 |
According to Eq. (140), the work performed by the spring force on the mass
as it moves from displacement 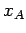 to
to 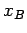 is
is
![\begin{displaymath}
W = \int_{x_A}^{x_B} f(x) dx = -k\int_{x_A}^{x_B} x dx = -...
...
\frac{1}{2} k x_B^{ 2} -\frac{1}{2} k x_A^{ 2} \right].
\end{displaymath}](img674.png) |
(160) |
Note that the right-hand side of the above expression consists of the difference
between two factors: the first only depends on the final state of the mass, whereas the
second only depends on its initial state. This is a sure sign that it is
possible to associate a potential energy with the spring force.
Equation (155), which is the basic definition of potential
energy, yields
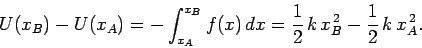 |
(161) |
Hence, the potential energy of the mass takes the form
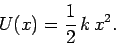 |
(162) |
Note that the above potential energy actually represents energy stored by the
spring--in
the form of mechanical stresses--when it is either
stretched or compressed. Incidentally, this energy must be stored without loss, otherwise
the concept of potential energy would be meaningless. It follows that the spring
force is another example of a conservative force.
It is reasonable to suppose that the form of the spring potential energy is somehow related to the
form of the spring force. Let us now explicitly investigate this
relationship. If we let
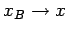 and
and
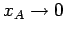 then Eq. (161)
gives
then Eq. (161)
gives
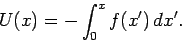 |
(163) |
We can differentiate this expression to obtain
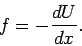 |
(164) |
Thus, in 1-dimension, a conservative force is equal to minus the derivative (with respect
to displacement) of its associated potential energy. This is a quite general result.
For the case of a
spring force:
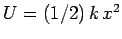 , so
, so
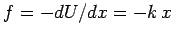 .
.
As is easily demonstrated, the 3-dimensional equivalent to Eq. (164) is
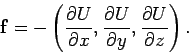 |
(165) |
For example, we have seen that the gravitational potential energy of
a mass 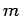 moving above the Earth's surface is
moving above the Earth's surface is 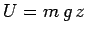 ,
where
,
where 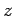 measures height off the ground. It follows that the
associated gravitational force is
measures height off the ground. It follows that the
associated gravitational force is
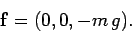 |
(166) |
In other words, the force is of magnitude 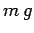 , and is directed
vertically downward.
, and is directed
vertically downward.
The total energy of the mass shown in Fig. 42 is the sum of its kinetic and
potential energies:
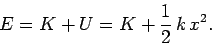 |
(167) |
Of course, 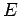 remains constant during the
mass's motion. Hence, the above expression can be rearranged
to give
remains constant during the
mass's motion. Hence, the above expression can be rearranged
to give
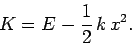 |
(168) |
Since it is impossible
for a kinetic energy
to be negative, the above expression
suggests that 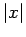 can never exceed the value
can never exceed the value
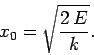 |
(169) |
Here, 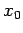 is termed the amplitude of the mass's motion. Note that when
is termed the amplitude of the mass's motion. Note that when
 attains its maximum value
attains its maximum value 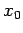 , or its minimum value
, or its minimum value 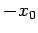 , the
kinetic energy is momentarily zero (i.e.,
, the
kinetic energy is momentarily zero (i.e., 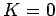 ).
).



Next: Motion in a general
Up: Conservation of energy
Previous: Potential energy
Richard Fitzpatrick
2006-02-02
![]() to
to ![]() is
is
![]() and
and
![]() then Eq. (161)
gives
then Eq. (161)
gives