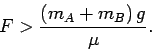Next: Conservation of energy
Up: Newton's laws of motion
Previous: Worked example 4.3: Raising
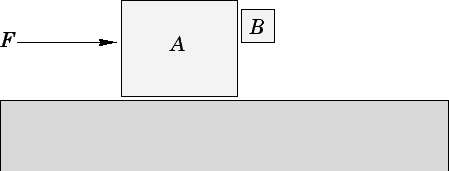
Question: Consider the diagram. The mass of block  is
is 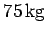 and
the mass of block
and
the mass of block  is
is 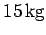 . The coefficient of static friction
between the two blocks is
. The coefficient of static friction
between the two blocks is 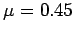 . The horizontal surface is frictionless. What
minimum force
. The horizontal surface is frictionless. What
minimum force
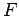 must be exerted on block
must be exerted on block  in order to prevent block
in order to prevent block  from
falling?
from
falling?
Answer: Suppose that block  exerts a rightward force
exerts a rightward force  on block
on block  . By Newton's third law, block
. By Newton's third law, block  exerts an equal and opposite force
on block
exerts an equal and opposite force
on block  . Applying Newton's second law of motion to the rightward
acceleration
. Applying Newton's second law of motion to the rightward
acceleration  of block
of block  , we obtain
, we obtain
where 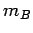 is the mass of block
is the mass of block  . The normal reaction at the interface between
the two blocks is
. The normal reaction at the interface between
the two blocks is  . Hence, the maximum frictional force that block
. Hence, the maximum frictional force that block  can exert on block
can exert on block  is
is 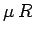 . In order to prevent block
. In order to prevent block  from falling,
this maximum frictional force (which acts upwards) must exceed the downward acting weight,
from falling,
this maximum frictional force (which acts upwards) must exceed the downward acting weight, 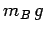 ,
of the block. Hence, we require
,
of the block. Hence, we require
or
Applying Newton's second law to the rightward acceleration  of both blocks (remembering that the
equal and opposite forces exerted between the blocks cancel one another out), we obtain
of both blocks (remembering that the
equal and opposite forces exerted between the blocks cancel one another out), we obtain
where  is the mass of block
is the mass of block  . It follows that
. It follows that
Since
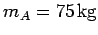 ,
,
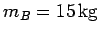 , and
, and 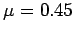 , we have
, we have



Next: Conservation of energy
Up: Newton's laws of motion
Previous: Worked example 4.3: Raising
Richard Fitzpatrick
2006-02-02

![]() exerts a rightward force
exerts a rightward force ![]() on block
on block ![]() . By Newton's third law, block
. By Newton's third law, block ![]() exerts an equal and opposite force
on block
exerts an equal and opposite force
on block ![]() . Applying Newton's second law of motion to the rightward
acceleration
. Applying Newton's second law of motion to the rightward
acceleration ![]() of block
of block ![]() , we obtain
, we obtain