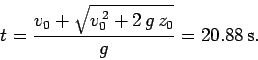Next: Worked example 3.4: Hail
Up: Motion in 3 dimensions
Previous: Worked example 3.2: Gallileo's
Question: A cannon placed on a 50m high cliff
fires a cannonball over the edge of the cliff at
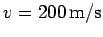 making an angle
of
making an angle
of
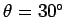 to the horizontal. How long is the cannonball in the air? Neglect
air resistance.
to the horizontal. How long is the cannonball in the air? Neglect
air resistance.
Answer: In order to answer this question we need only consider the cannonball's
vertical motion. At  (i.e., the time of firing) the cannonball's height off the
ground is
(i.e., the time of firing) the cannonball's height off the
ground is 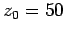 m and its velocity component in the vertical direction is
m and its velocity component in the vertical direction is
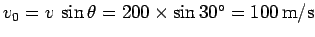 . Moreover,
the cannonball is accelerating vertically downwards at
. Moreover,
the cannonball is accelerating vertically downwards at
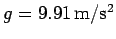 .
The equation of vertical motion of the cannonball is written
.
The equation of vertical motion of the cannonball is written
where  is the cannonball's height off the ground at time
is the cannonball's height off the ground at time  . The time of flight
of the cannonball corresponds to the time
. The time of flight
of the cannonball corresponds to the time  at which
at which 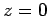 . In other words,
the time of flight is the solution of the quadratic equation
. In other words,
the time of flight is the solution of the quadratic equation
Hence,
Here, we have neglected the unphysical negative root of our quadratic equation.



Next: Worked example 3.4: Hail
Up: Motion in 3 dimensions
Previous: Worked example 3.2: Gallileo's
Richard Fitzpatrick
2006-02-02