Next: Motion in 3 dimensions
Up: Motion in 1 dimension
Previous: Worked example 2.2: Speed
Question: In 1886, Steve Brodie achieved notoriety by allegedly jumping off
the recently completed Brooklyn bridge, for a bet, and surviving. Given
that the bridge rises 135ft over the East River, how long would Mr. Brodie have
been in the air, and with what speed would he have struck the water? Give
all answers in mks units. You may neglect air resistance.
Answer: Mr. Brodie's net vertical
displacement was
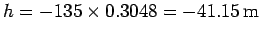 .
Assuming that his initial velocity was zero,
.
Assuming that his initial velocity was zero,
where  was his time of flight. Hence,
was his time of flight. Hence,
His final velocity was
Thus, the speed with which he plunged into the East River was
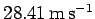 , or
, or
 ! Clearly,
Mr. Brodie's story should be taken with a pinch of salt.
! Clearly,
Mr. Brodie's story should be taken with a pinch of salt.
Richard Fitzpatrick
2006-02-02