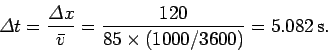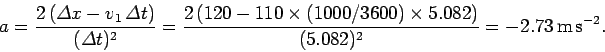Next: Worked example 2.3: The
Up: Motion in 1 dimension
Previous: Worked example 2.1: Velocity-time
Question: In a speed trap, two pressure-activated strips are placed 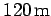 apart on a highway on which the speed limit is
apart on a highway on which the speed limit is
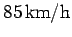 . A driver going
. A driver going
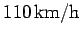 notices a police car just as he/she activates the first strip, and immediately slows down. What
deceleration is needed so that the car's average speed is within the speed limit
when the car crosses the second strip?
notices a police car just as he/she activates the first strip, and immediately slows down. What
deceleration is needed so that the car's average speed is within the speed limit
when the car crosses the second strip?
Answer: Let
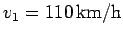 be the speed of the car at the first strip.
Let
be the speed of the car at the first strip.
Let
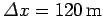 be the
distance between the two strips, and let
be the
distance between the two strips, and let
 be the time taken by the
car to travel from one strip to the other. The average velocity of the car is
be the time taken by the
car to travel from one strip to the other. The average velocity of the car is
We need this velocity to be
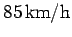 . Hence, we require
. Hence, we require
Here, we have changed units from 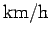 to
to 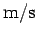 . Now,
assuming that the acceleration
. Now,
assuming that the acceleration  of the car is uniform, we have
of the car is uniform, we have
which can be rearranged to give
Hence, the required deceleration is
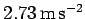 .
.



Next: Worked example 2.3: The
Up: Motion in 1 dimension
Previous: Worked example 2.1: Velocity-time
Richard Fitzpatrick
2006-02-02