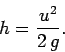Next: Worked example 2.1: Velocity-time
Up: Motion in 1 dimension
Previous: Motion with constant acceleration
Galileo Galilei was the first scientist to appreciate that, neglecting the
effect of air resistance, all bodies in free-fall close to the Earth's
surface accelerate vertically downwards with the same acceleration: namely,
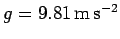 .1The neglect of air resistance is a fairly good approximation for large objects
which travel relatively slowly (e.g., a shot-putt, or a basketball), but
becomes a poor approximation for small objects which travel relatively rapidly
(e.g., a golf-ball, or a bullet fired from a pistol).
.1The neglect of air resistance is a fairly good approximation for large objects
which travel relatively slowly (e.g., a shot-putt, or a basketball), but
becomes a poor approximation for small objects which travel relatively rapidly
(e.g., a golf-ball, or a bullet fired from a pistol).
Equations (21)-(23) can easily be modified to deal with the
special case of an object free-falling under gravity:
Here,
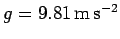 is the downward acceleration due to gravity,
is the downward acceleration due to gravity,  is the
distance the object has moved vertically between times
is the
distance the object has moved vertically between times  and
and  (if
(if 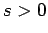 then the object has
risen
then the object has
risen  meters, else if
meters, else if 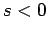 then the object has
fallen
then the object has
fallen 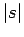 meters), and
meters), and 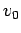 is the object's instantaneous velocity at
is the object's instantaneous velocity at  . Finally,
. Finally,
 is the object's instantaneous velocity at time
is the object's instantaneous velocity at time  .
.
Let us illustrate the use of Eqs. (24)-(26). Suppose that
a ball is released from rest and allowed to fall under the influence of gravity.
How long does it take the ball to fall 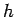 meters? Well, according to Eq. (24)
[with
meters? Well, according to Eq. (24)
[with 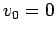 (since the ball is released from rest), and
(since the ball is released from rest), and 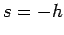 (since we wish the
ball to fall
(since we wish the
ball to fall 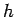 meters)],
meters)], 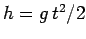 , so the time of fall is
, so the time of fall is
 |
(27) |
Suppose that a ball is thrown vertically upwards from ground level with velocity  .
To what height does the ball rise,
how
long does it remain in the air, and with what velocity does it strike the
ground? The ball attains its maximum height when it is momentarily at rest
(i.e., when
.
To what height does the ball rise,
how
long does it remain in the air, and with what velocity does it strike the
ground? The ball attains its maximum height when it is momentarily at rest
(i.e., when  ). According to Eq. (25) (with
). According to Eq. (25) (with 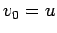 ),
this occurs at time
),
this occurs at time 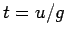 . It follows from Eq. (24) (with
. It follows from Eq. (24) (with
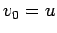 , and
, and 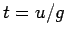 ) that the maximum height of the ball
is given by
) that the maximum height of the ball
is given by
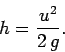 |
(28) |
When the ball strikes the ground it has traveled zero net meters vertically, so 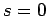 .
It follows from Eqs. (25) and (26) (with
.
It follows from Eqs. (25) and (26) (with 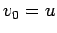 and
and 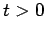 ) that
) that 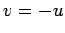 .
In other words, the ball hits the ground with an equal and opposite velocity to that
with
which it was thrown into the air. Since the ascent and decent phases of the ball's
trajectory are clearly symmetric, the ball's time of flight is
simply twice the time required for the ball to attain its maximum height:
i.e.,
.
In other words, the ball hits the ground with an equal and opposite velocity to that
with
which it was thrown into the air. Since the ascent and decent phases of the ball's
trajectory are clearly symmetric, the ball's time of flight is
simply twice the time required for the ball to attain its maximum height:
i.e.,
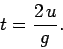 |
(29) |



Next: Worked example 2.1: Velocity-time
Up: Motion in 1 dimension
Previous: Motion with constant acceleration
Richard Fitzpatrick
2006-02-02
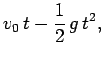
![]() meters? Well, according to Eq. (24)
[with
meters? Well, according to Eq. (24)
[with ![]() (since the ball is released from rest), and
(since the ball is released from rest), and ![]() (since we wish the
ball to fall
(since we wish the
ball to fall ![]() meters)],
meters)], ![]() , so the time of fall is
, so the time of fall is
![]() .
To what height does the ball rise,
how
long does it remain in the air, and with what velocity does it strike the
ground? The ball attains its maximum height when it is momentarily at rest
(i.e., when
.
To what height does the ball rise,
how
long does it remain in the air, and with what velocity does it strike the
ground? The ball attains its maximum height when it is momentarily at rest
(i.e., when ![]() ). According to Eq. (25) (with
). According to Eq. (25) (with ![]() ),
this occurs at time
),
this occurs at time ![]() . It follows from Eq. (24) (with
. It follows from Eq. (24) (with
![]() , and
, and ![]() ) that the maximum height of the ball
is given by
) that the maximum height of the ball
is given by