| (559) |
Suppose that the satellite's orbit lies in the Earth's equatorial plane. Moreover, suppose that the satellite's orbital angular velocity just matches the Earth's angular velocity of rotation. In this case, the satellite will appear to hover in the same place in the sky to a stationary observer on the Earth's surface. A satellite with this singular property is known as a geostationary satellite.
Virtually all of the satellites used to monitor the Earth's weather patterns are geostationary in nature. Communications satellites also tend to be geostationary. Of course, the satellites which beam satellite-TV to homes across the world must be geostationary--otherwise, you would need to install an expensive tracking antenna on top of your house in order to pick up the transmissions. Incidentally, the person who first envisaged rapid global telecommunication via a network of geostationary satellites was the science fiction writer Arthur C. Clarke in 1945.
Let us calculate the orbital radius of a geostationary satellite. The angular
velocity of the Earth's rotation is
| (560) |
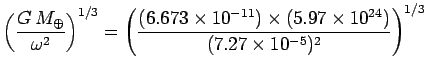 |
|||
| (561) |