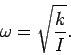Next: The simple pendulum
Up: Oscillatory motion
Previous: Simple harmonic motion
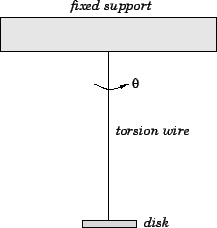
Consider a disk suspended from a torsion wire attached to its centre. See Fig. 96. This setup is known as a torsion
pendulum.
A torsion wire is essentially inextensible, but is free to twist about its axis.
Of course, as the wire twists it also causes the disk attached to it to rotate in the horizontal
plane. Let  be the angle of rotation of the disk, and let
be the angle of rotation of the disk, and let 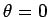 correspond to the case in which the wire is untwisted.
correspond to the case in which the wire is untwisted.
Figure 96:
A torsion pendulum.
 |
Any twisting of the wire is inevitably associated with mechanical deformation. The wire resists such deformation by developing
a restoring torque, 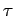 , which acts to restore the wire to its untwisted state. For relatively small angles
of twist, the magnitude of this torque is directly proportional to the twist angle. Hence, we can write
, which acts to restore the wire to its untwisted state. For relatively small angles
of twist, the magnitude of this torque is directly proportional to the twist angle. Hence, we can write
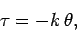 |
(518) |
where 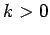 is the torque constant of the wire. The above equation is essentially a torsional
equivalent to Hooke's law. The rotational equation of motion of the system is
written
is the torque constant of the wire. The above equation is essentially a torsional
equivalent to Hooke's law. The rotational equation of motion of the system is
written
 |
(519) |
where 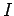 is the moment of inertia of the disk (about a perpendicular axis through its centre). The moment
of inertia of the wire is assumed to be negligible. Combining the previous two equations, we obtain
is the moment of inertia of the disk (about a perpendicular axis through its centre). The moment
of inertia of the wire is assumed to be negligible. Combining the previous two equations, we obtain
 |
(520) |
Equation (520) is clearly a simple harmonic equation [cf., Eq. (504)]. Hence,
we can immediately write the standard solution [cf., Eq. (505)]
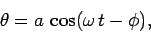 |
(521) |
where [cf., Eq. (507)]
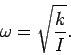 |
(522) |
We conclude that when a torsion pendulum is perturbed from its equilibrium state (i.e., 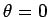 ),
it executes torsional oscillations about this state at a fixed frequency,
),
it executes torsional oscillations about this state at a fixed frequency,  , which
depends only on the torque constant of the wire and the moment of inertia of the disk. Note,
in particular, that the frequency is independent of the amplitude of the oscillation [provided
, which
depends only on the torque constant of the wire and the moment of inertia of the disk. Note,
in particular, that the frequency is independent of the amplitude of the oscillation [provided  remains small enough that Eq. (518) still applies]. Torsion pendulums are often
used for time-keeping purposes. For instance, the balance wheel in a mechanical wristwatch is a torsion
pendulum in which the restoring torque is provided by a coiled spring.
remains small enough that Eq. (518) still applies]. Torsion pendulums are often
used for time-keeping purposes. For instance, the balance wheel in a mechanical wristwatch is a torsion
pendulum in which the restoring torque is provided by a coiled spring.



Next: The simple pendulum
Up: Oscillatory motion
Previous: Simple harmonic motion
Richard Fitzpatrick
2006-02-02

![]() , which acts to restore the wire to its untwisted state. For relatively small angles
of twist, the magnitude of this torque is directly proportional to the twist angle. Hence, we can write
, which acts to restore the wire to its untwisted state. For relatively small angles
of twist, the magnitude of this torque is directly proportional to the twist angle. Hence, we can write