


Next: Worked example 10.5: Rod
Up: Statics
Previous: Worked example 10.3: Leaning
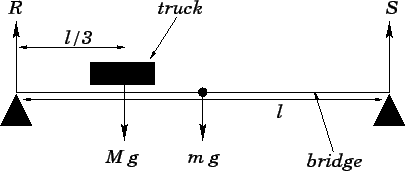
Question: A truck of mass
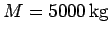 is crossing
a uniform horizontal bridge of mass
is crossing
a uniform horizontal bridge of mass
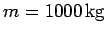 and length
and length
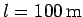 .
The bridge is supported at its two end-points. What are the reactions
at these supports when the truck is one third of the way across the bridge?
.
The bridge is supported at its two end-points. What are the reactions
at these supports when the truck is one third of the way across the bridge?
Answer: Let  and
and 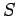 be the reactions at the bridge supports.
Here,
be the reactions at the bridge supports.
Here,  is the reaction at the support closest to the truck. Setting the net vertical
force acting on the bridge to zero, we obtain
is the reaction at the support closest to the truck. Setting the net vertical
force acting on the bridge to zero, we obtain
Setting the torque acting on the bridge about the left-most support to zero,
we get
Here, we have made use of the fact that centre of mass of the bridge lies at its
mid-point. It follows from the above two equations that
and



Next: Worked example 10.5: Rod
Up: Statics
Previous: Worked example 10.3: Leaning
Richard Fitzpatrick
2006-02-02

![]() and
and ![]() be the reactions at the bridge supports.
Here,
be the reactions at the bridge supports.
Here, ![]() is the reaction at the support closest to the truck. Setting the net vertical
force acting on the bridge to zero, we obtain
is the reaction at the support closest to the truck. Setting the net vertical
force acting on the bridge to zero, we obtain