


Next: Angular momentum of an
Up: Angular momentum
Previous: Introduction
Angular momentum of a point particle
Consider a particle of mass  , position vector
, position vector  , and instantaneous velocity
, and instantaneous velocity 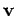 ,
which rotates about an axis
passing through the origin of our coordinate system. We know that the
particle's linear momentum is written
,
which rotates about an axis
passing through the origin of our coordinate system. We know that the
particle's linear momentum is written
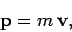 |
(414) |
and satisfies
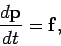 |
(415) |
where 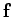 is the force acting on the particle. Let us search for the rotational
equivalent of
is the force acting on the particle. Let us search for the rotational
equivalent of 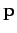 .
.
Consider the quantity
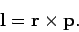 |
(416) |
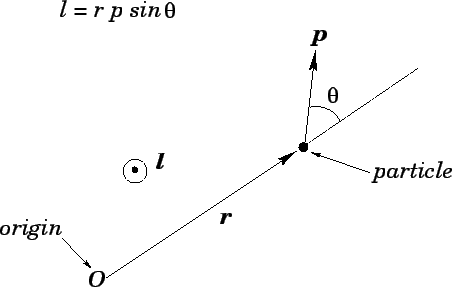
This quantity--which is known as angular momentum--is a vector of magnitude
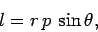 |
(417) |
where  is the angle subtended between the directions of
is the angle subtended between the directions of  and
and 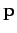 .
The direction of
.
The direction of 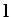 is defined to be mutually perpendicular to the directions
of
is defined to be mutually perpendicular to the directions
of  and
and 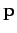 , in the sense given by the right-hand grip rule. In other
words, if vector
, in the sense given by the right-hand grip rule. In other
words, if vector  rotates onto vector
rotates onto vector 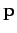 (through an angle less
than
(through an angle less
than 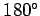 ), and the fingers of the right-hand are aligned with this rotation, then
the thumb of the right-hand indicates the direction of
), and the fingers of the right-hand are aligned with this rotation, then
the thumb of the right-hand indicates the direction of 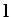 . See Fig. 85.
. See Fig. 85.
Figure 85:
Angular momentum of a point particle about the origin.
 |
Let us differentiate Eq. (416) with respect to time. We obtain
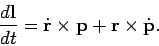 |
(418) |
Note that the derivative of a vector product is formed in much the same manner as
the derivative of an ordinary product, except that the order of the various terms is
preserved. Now, we know that
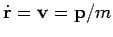 and
and
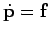 .
Hence, we obtain
.
Hence, we obtain
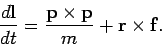 |
(419) |
However,
 , since the vector product of two parallel
vectors is zero. Also,
, since the vector product of two parallel
vectors is zero. Also,
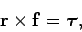 |
(420) |
where
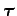 is the torque acting on the particle about an axis passing through the
origin. We conclude that
is the torque acting on the particle about an axis passing through the
origin. We conclude that
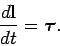 |
(421) |
Of course, this equation is analogous to Eq. (415), which suggests that angular
momentum, 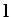 , plays the role of linear momentum,
, plays the role of linear momentum, 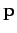 , in rotational
dynamics.
, in rotational
dynamics.
For the special case of a particle of mass  executing a circular orbit of radius
executing a circular orbit of radius  ,
with instantaneous velocity
,
with instantaneous velocity  and instantaneous angular velocity
and instantaneous angular velocity  , the
magnitude of the particle's angular momentum is simply
, the
magnitude of the particle's angular momentum is simply
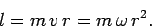 |
(422) |



Next: Angular momentum of an
Up: Angular momentum
Previous: Introduction
Richard Fitzpatrick
2006-02-02
![]() executing a circular orbit of radius
executing a circular orbit of radius ![]() ,
with instantaneous velocity
,
with instantaneous velocity ![]() and instantaneous angular velocity
and instantaneous angular velocity ![]() , the
magnitude of the particle's angular momentum is simply
, the
magnitude of the particle's angular momentum is simply