


Next: Determination of Equinox and
Up: The Sun
Previous: Determination of Ecliptic Longitude
Example 1: May 5, 2005 CE, 00:00 UT:
According to Tables 27-29,
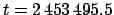 JD. Hence,
JD. Hence,
 JD. Making use of
Table 32, we find:
JD. Making use of
Table 32, we find:
| |
|
|
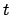 (JD) (JD) |
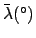 |
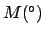 |
| |
|
|
| +1000 |
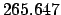 |
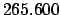 |
| +900 |
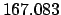 |
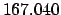 |
| +50 |
 |
 |
| +.5 |
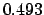 |
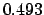 |
| Epoch |
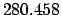 |
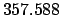 |
| |
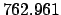 |
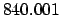 |
| Modulus |
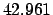 |
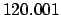 |
| |
|
|
Rounding the mean anomaly to the nearest degree, we obtain
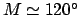 .
It follows from Table 33 that
.
It follows from Table 33 that
so
Here, we have converted the decimal fraction into arc
minutes using Table 31, and
then rounded the final result to the nearest arc minute.
Following
the practice of the Ancient Greeks (and modern-day astrologers), we shall express ecliptic longitudes
in terms of the signs of the zodiac, which are listed in Sect. 2.6. The ecliptic longitude 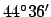 is conventionally written 14TA36: i.e.,
is conventionally written 14TA36: i.e.,
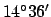 into the sign of Taurus. Thus, we conclude that the position of
the sun
at 00:00 UT on May 5, 2005 CE was 14TA36.
into the sign of Taurus. Thus, we conclude that the position of
the sun
at 00:00 UT on May 5, 2005 CE was 14TA36.
Example 2: December 25, 1800 CE, 00:00 UT:
According to Tables 27-29,
 JD. Hence,
JD. Hence,
 JD. Making use of
Table 32, we find:
JD. Making use of
Table 32, we find:
| |
|
|
 (JD) (JD) |
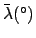 |
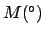 |
| |
|
|
| -70,000 |
 |
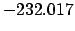 |
| -2,000 |
 |
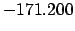 |
| -600 |
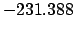 |
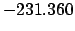 |
| -90 |
 |
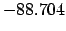 |
| -.5 |
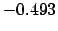 |
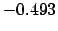 |
| Epoch |
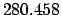 |
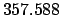 |
| |
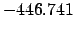 |
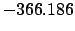 |
| Modulus |
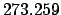 |
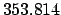 |
| |
|
|
We conclude that
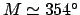 .
From Table 33,
.
From Table 33,
so
Thus, the position of the sun at 00:00 UT on December 25, 1800 CE was 3CP03.



Next: Determination of Equinox and
Up: The Sun
Previous: Determination of Ecliptic Longitude
Richard Fitzpatrick
2010-07-21
![]() is conventionally written 14TA36: i.e.,
is conventionally written 14TA36: i.e.,
![]() into the sign of Taurus. Thus, we conclude that the position of
the sun
at 00:00 UT on May 5, 2005 CE was 14TA36.
into the sign of Taurus. Thus, we conclude that the position of
the sun
at 00:00 UT on May 5, 2005 CE was 14TA36.
![]() JD. Hence,
JD. Hence,
![]() JD. Making use of
Table 32, we find:
JD. Making use of
Table 32, we find: