

Next: Mercury
Up: Planetary Latitudes
Previous: Determination of Ecliptic Latitude
The ecliptic latitude of Venus can be determined with the aid of Tables 58, 73, and 74. Table 58 allows
the mean argument of latitude, 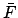 , of Venus to be calculated as a function of
time. Next, Table 73 permits the epicyclic latitude,
, of Venus to be calculated as a function of
time. Next, Table 73 permits the epicyclic latitude, 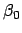 , to
be determined as a function of the true argument of latitude,
, to
be determined as a function of the true argument of latitude, 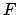 . Finally, Table 74 allows the quantities
. Finally, Table 74 allows the quantities
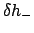 ,
, 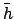 , and
, and 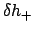 to be calculated as functions of the epicyclic
anomaly,
to be calculated as functions of the epicyclic
anomaly,  .
.
The procedure for using the tables is as follows:
- Determine the fractional Julian day number,
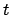 , corresponding to the date and time
at which the ecliptic latitude is to be calculated with the aid of Tables 27-29. Form
, corresponding to the date and time
at which the ecliptic latitude is to be calculated with the aid of Tables 27-29. Form
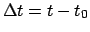 , where
, where
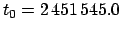 is the epoch.
is the epoch.
- Calculate the planetary equation
of center,
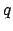 , ecliptic anomaly,
, ecliptic anomaly,  , and
interpolation parameters
, and
interpolation parameters 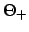 and
and  using the
procedure set out in Cha. 9.
using the
procedure set out in Cha. 9.
- Enter Table 58 with the digit for each power of 10
in
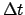 and take out the corresponding values of
and take out the corresponding values of 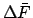 . If
. If 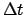 is negative then the corresponding
values are also negative.
The value of the mean argument of latitude,
is negative then the corresponding
values are also negative.
The value of the mean argument of latitude, 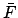 , is the
sum of all the
, is the
sum of all the 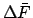 values plus the value of
values plus the value of 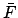 at the epoch.
at the epoch.
- Form the true argument of latitude,
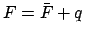 . Add as many multiples of
. Add as many multiples of 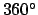 to
to 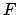 as is required to make it fall in the range
as is required to make it fall in the range 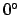 to
to 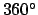 .
Round
.
Round 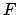 to the nearest degree.
to the nearest degree.
- Enter Table 73 with the value of
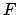 and take out the
corresponding value of the epicyclic latitude,
and take out the
corresponding value of the epicyclic latitude, 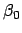 . It is necessary to interpolate if
. It is necessary to interpolate if 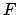 is odd.
is odd.
- Enter Table 74 with the value of
 and take
out the corresponding values of
and take
out the corresponding values of 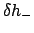 ,
, 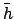 , and
, and
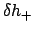 . If
. If
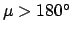 then it is necessary to make use
of the identities
then it is necessary to make use
of the identities
 and
and
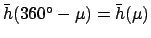 .
.
- Form the deferential latitude correction factor,
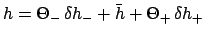 .
.
- The ecliptic latitude,
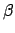 , is the product of the epicyclic latitude,
, is the product of the epicyclic latitude,
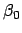 , and the deferential latitude correction factor,
, and the deferential latitude correction factor, 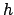 . The decimal fraction can
be converted into arc minutes
using Table 31. Round to the nearest arc minute.
. The decimal fraction can
be converted into arc minutes
using Table 31. Round to the nearest arc minute.
One example of this procedure is given below.
Example: May 5, 2005 CE, 00:00 UT:
From Cha. 9,
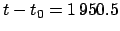 JD,
JD,
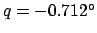 ,
,
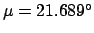 ,
,
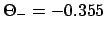 , and
, and
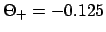 .
Making use of
Table 58, we find:
.
Making use of
Table 58, we find:
| |
|
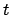 (JD) (JD) |
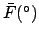 |
| |
|
| +1000 |
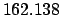 |
| +900 |
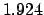 |
| +50 |
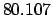 |
| +.5 |
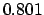 |
| Epoch |
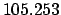 |
| |
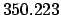 |
| Modulus |
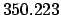 |
| |
|
Thus,
It follows from Table 73 that
Since
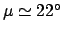 , Table 74 yields
, Table 74 yields
so
Finally,
Thus,
the ecliptic latitude of Venus at 00:00 UT on May 5, 2005 CE was 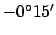 .
.


Next: Mercury
Up: Planetary Latitudes
Previous: Determination of Ecliptic Latitude
Richard Fitzpatrick
2010-07-21
![]() JD,
JD,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() .
Making use of
Table 58, we find:
.
Making use of
Table 58, we find: