

Next: Solar and Lunar Eclipses
Up: Lunar-Solar Syzygies and Eclipses
Previous: Determination of Lunar-Solar Elongation
Example 1: Sixth new moon in 2004 CE:
From Table 42, the date of first new moon in 2004 CE is 2453026.4 JD. Now, the
lunar-solar elongation increases at the mean rate
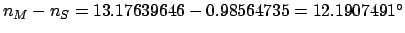 per day, or
per day, or
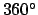 in
in 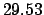 days--the latter time period is known as a synodic month. Hence, a rough estimate for the
date of the sixth new moon in 2004 CE is five synodic months after that of the first: i.e.,
days--the latter time period is known as a synodic month. Hence, a rough estimate for the
date of the sixth new moon in 2004 CE is five synodic months after that of the first: i.e.,
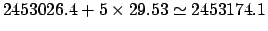 JD. It follows that
JD. It follows that
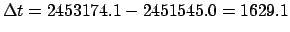 JD. Let us calculate the lunar-solar elongation at this date.
From Table 40:
JD. Let us calculate the lunar-solar elongation at this date.
From Table 40:
| |
|
|
|
|
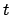 (JD) (JD) |
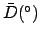 |
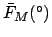 |
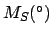 |
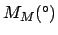 |
| |
|
|
|
|
| +1000 |
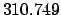 |
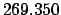 |
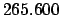 |
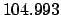 |
| +600 |
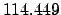 |
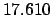 |
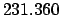 |
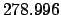 |
| +20 |
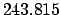 |
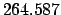 |
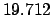 |
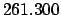 |
| +9 |
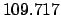 |
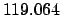 |
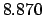 |
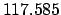 |
| +.1 |
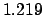 |
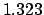 |
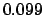 |
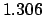 |
| Epoch |
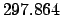 |
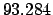 |
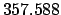 |
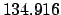 |
| |
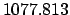 |
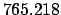 |
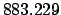 |
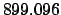 |
| Modulus |
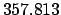 |
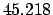 |
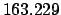 |
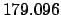 |
| |
|
|
|
|
Thus,
Table 41 yields
Hence,
Now, the actual new moon takes place when
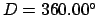 . Thus, a far better estimate for the date
of the sixth new moon in 2004 CE is
. Thus, a far better estimate for the date
of the sixth new moon in 2004 CE is
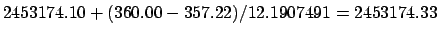 JD.
This corresponds to 20:00 UT on June 17th.
JD.
This corresponds to 20:00 UT on June 17th.
Example 2: Third full moon in 1982 CE:
From Table 42, the fractional Julian day number of first new moon in 1982 CE is 2444994.7 JD, which
corresponds to January 25th. Since there is more than half a synodic month between this event and the
start of year, we conclude that the first full moon in 1982 CE took place before January 25th. Hence, a rough estimate for the
date of the third full moon in 1982 CE is one and a half synodic months after that of the first new moon: i.e.,
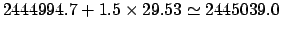 JD. It follows that
JD. It follows that
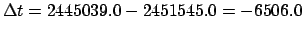 JD. Let us calculate the lunar-solar elongation at
this date.
From Table 40:
JD. Let us calculate the lunar-solar elongation at
this date.
From Table 40:
| |
|
|
|
|
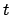 (JD) (JD) |
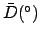 |
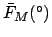 |
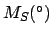 |
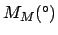 |
| |
|
|
|
|
| -6000 |
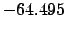 |
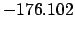 |
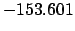 |
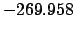 |
| -500 |
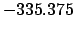 |
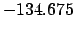 |
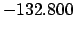 |
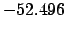 |
| -6 |
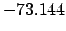 |
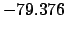 |
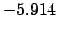 |
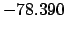 |
| Epoch |
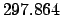 |
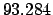 |
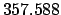 |
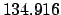 |
| |
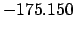 |
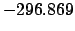 |
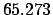 |
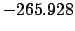 |
| Modulus |
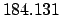 |
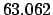 |
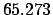 |
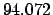 |
| |
|
|
|
|
Thus,
Table 41 yields
Hence,
Now, the actual full moon takes place when
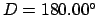 . Thus, a far better estimate for the date
of the third full moon in 1982 CE is
. Thus, a far better estimate for the date
of the third full moon in 1982 CE is
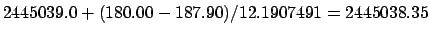 JD.
This corresponds to 20:00 UT on March 9th.
JD.
This corresponds to 20:00 UT on March 9th.


Next: Solar and Lunar Eclipses
Up: Lunar-Solar Syzygies and Eclipses
Previous: Determination of Lunar-Solar Elongation
Richard Fitzpatrick
2010-07-21
![]() JD. It follows that
JD. It follows that
![]() JD. Let us calculate the lunar-solar elongation at
this date.
From Table 40:
JD. Let us calculate the lunar-solar elongation at
this date.
From Table 40: