


Next: Hydrostatic equilibrium of the
Up: Classical thermodynamics
Previous: Calculation of specific heats
Suppose that the temperature of an ideal
gas is held constant by keeping the gas in thermal
contact with a heat reservoir. If the gas is allowed to expand quasi-statically
under these so called isothermal conditions then the ideal equation of state
tells us that
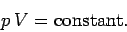 |
(311) |
This is usually called the isothermal gas law.
Suppose, now, that the gas is thermally isolated from its surroundings. If
the gas is allowed to expand quasi-statically under these so called
adiabatic
conditions then
it does work on its environment, and, hence, its internal energy is reduced,
and its temperature changes. Let us work out the relationship between the
pressure and volume of the gas during adiabatic expansion.
According to the first law of thermodynamics,
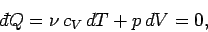 |
(312) |
in an adiabatic process (in which no heat is absorbed). The ideal gas
equation
of state can be differentiated, yielding
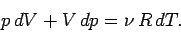 |
(313) |
The temperature increment  can be eliminated between the above two expressions
to give
can be eliminated between the above two expressions
to give
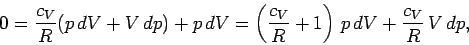 |
(314) |
which reduces to
 |
(315) |
Dividing through by 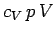 yields
yields
 |
(316) |
where
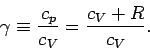 |
(317) |
It turns out that 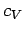 is a very slowly varying function of temperature in most
gases. So, it is always a fairly good approximation to treat the ratio
of specific heats
is a very slowly varying function of temperature in most
gases. So, it is always a fairly good approximation to treat the ratio
of specific heats 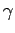 as a constant, at least over a limited temperature
range. If
as a constant, at least over a limited temperature
range. If 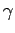 is constant then we can integrate Eq. (316) to give
is constant then we can integrate Eq. (316) to give
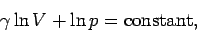 |
(318) |
or
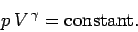 |
(319) |
This is the famous adiabatic gas law.
It is very easy to obtain similar relationships between 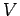 and
and  and
and 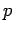 and
and  during adiabatic expansion or contraction. Since
during adiabatic expansion or contraction. Since
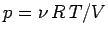 , the above formula
also implies that
, the above formula
also implies that
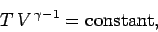 |
(320) |
and
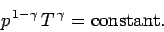 |
(321) |
Equations (319)-(321) are all completely equivalent.



Next: Hydrostatic equilibrium of the
Up: Classical thermodynamics
Previous: Calculation of specific heats
Richard Fitzpatrick
2006-02-02