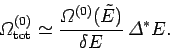Next: Uses of entropy
Up: Statistical thermodynamics
Previous: Entropy
Properties of entropy
Entropy, as we have defined it, has some dependence on the resolution 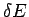 to which the energy of macrostates is measured. Recall that
to which the energy of macrostates is measured. Recall that
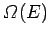 is the
number of accessible microstates with energy in the range
is the
number of accessible microstates with energy in the range  to
to  .
Suppose that we choose a new resolution
.
Suppose that we choose a new resolution 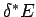 and define a new
density of states
and define a new
density of states
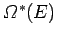 which is the number of states with energy
in the range
which is the number of states with energy
in the range  to
to
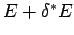 . It can easily be seen that
. It can easily be seen that
 |
(227) |
It follows that the new entropy
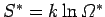 is related to the
previous entropy
is related to the
previous entropy
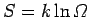 via
via
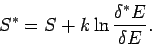 |
(228) |
Now, our usual estimate that
 gives
gives  , where
, where
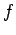 is the number of degrees of freedom. It follows that even if
is the number of degrees of freedom. It follows that even if 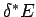 were to differ from
were to differ from 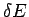 by of order
by of order 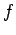 (i.e., twenty four orders of
magnitude), which is virtually inconceivable, the second term on the right-hand
side of the above equation is still only of order
(i.e., twenty four orders of
magnitude), which is virtually inconceivable, the second term on the right-hand
side of the above equation is still only of order 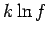 , which is utterly
negligible compared to
, which is utterly
negligible compared to 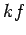 . It follows that
. It follows that
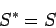 |
(229) |
to an excellent approximation, so our definition of entropy is completely
insensitive to the resolution to which we measure energy (or any other
macroscopic parameter).
Note that, like the
temperature, the entropy of a macrostate is only well-defined if
the macrostate is in equilibrium. The crucial point is that
it only makes sense to talk about the
number of accessible states if the systems
in the ensemble are given sufficient time to thoroughly explore all of the possible
microstates consistent with the known
macroscopic constraints. In other words, we can only
be sure that a given microstate is inaccessible when the systems in the ensemble have
had ample opportunity to move into it, and yet have not done so. Note that for an
equilibrium state, the entropy is just as well-defined as more familiar quantities
such as the temperature and the mean pressure.
Consider, again, two systems  and
and 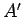 which are in thermal contact but can do
no work on one another (see Sect. 5.2).
Let
which are in thermal contact but can do
no work on one another (see Sect. 5.2).
Let  and
and 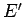 be the energies of the two systems,
and
be the energies of the two systems,
and
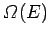 and
and
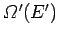 the respective densities of states.
Furthermore, let
the respective densities of states.
Furthermore, let 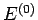 be the conserved energy of the
system as a whole and
be the conserved energy of the
system as a whole and
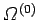 the corresponding density of states.
We have from Eq. (158) that
the corresponding density of states.
We have from Eq. (158) that
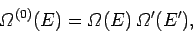 |
(230) |
where
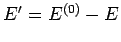 . In other words, the number of states accessible to the
whole system is the product of the numbers of states accessible to each subsystem,
since every microstate of
. In other words, the number of states accessible to the
whole system is the product of the numbers of states accessible to each subsystem,
since every microstate of  can be combined with every microstate of
can be combined with every microstate of
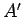 to form a distinct microstate of the whole system. We know, from Sect. 5.2,
that in equilibrium the mean energy of
to form a distinct microstate of the whole system. We know, from Sect. 5.2,
that in equilibrium the mean energy of  takes the value
takes the value
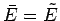 for which
for which
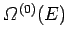 is maximum, and the
temperatures of
is maximum, and the
temperatures of  and
and 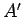 are equal. The distribution of
are equal. The distribution of  around the
mean value is of order
around the
mean value is of order
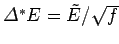 , where
, where 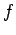 is the number of
degrees of freedom. It follows that the total number of accessible microstates is
approximately the number of states which lie within
is the number of
degrees of freedom. It follows that the total number of accessible microstates is
approximately the number of states which lie within
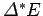 of
of 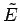 .
Thus,
.
Thus,
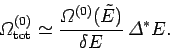 |
(231) |
The entropy of the whole system is given by
 |
(232) |
According to our usual estimate,
 , the first term on the
right-hand
side is of order
, the first term on the
right-hand
side is of order 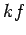 whereas the second term is of order
whereas the second term is of order
 . Any reasonable choice for the energy subdivision
. Any reasonable choice for the energy subdivision 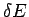 should be
greater than
should be
greater than  , otherwise there would
be less than one microstate per subdivision. It follows that the second term
is less than or of order
, otherwise there would
be less than one microstate per subdivision. It follows that the second term
is less than or of order 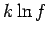 , which is utterly negligible compared to
, which is utterly negligible compared to
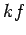 . Thus,
. Thus,
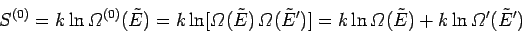 |
(233) |
to an excellent approximation,
giving
 |
(234) |
It can be seen that the probability distribution for
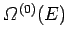 is so strongly peaked
around its maximum value that, for the purpose of calculating the entropy, the
total number of states is equal to the maximum number of states [i.e.,
is so strongly peaked
around its maximum value that, for the purpose of calculating the entropy, the
total number of states is equal to the maximum number of states [i.e.,
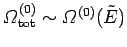 ].
One consequence
of this is that the entropy has the simple additive property shown in
Eq. (234). Thus, the total entropy of two thermally interacting systems
in equilibrium is the sum of the entropies of each system in isolation.
].
One consequence
of this is that the entropy has the simple additive property shown in
Eq. (234). Thus, the total entropy of two thermally interacting systems
in equilibrium is the sum of the entropies of each system in isolation.



Next: Uses of entropy
Up: Statistical thermodynamics
Previous: Entropy
Richard Fitzpatrick
2006-02-02
![]() and
and ![]() which are in thermal contact but can do
no work on one another (see Sect. 5.2).
Let
which are in thermal contact but can do
no work on one another (see Sect. 5.2).
Let ![]() and
and ![]() be the energies of the two systems,
and
be the energies of the two systems,
and
![]() and
and
![]() the respective densities of states.
Furthermore, let
the respective densities of states.
Furthermore, let ![]() be the conserved energy of the
system as a whole and
be the conserved energy of the
system as a whole and
![]() the corresponding density of states.
We have from Eq. (158) that
the corresponding density of states.
We have from Eq. (158) that