


Next: Combinatorial analysis
Up: Probability theory
Previous: Combining probabilities
The simplest non-trivial system which we can investigate using probability theory
is one for which there are only two
possible outcomes. There would obviously
be little
point in investigating a one outcome system. Let us
suppose that there are two possible outcomes to an observation made
on some system 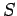 . Let us denote these outcomes 1 and 2, and let their
probabilities of occurrence be
. Let us denote these outcomes 1 and 2, and let their
probabilities of occurrence be
It follows immediately from the normalization condition (5) that
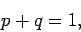 |
(11) |
so 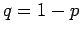 . The best known example of a two-state system is
a tossed coin. The two outcomes are ``heads'' and ``tails,'' each with
equal probabilities
. The best known example of a two-state system is
a tossed coin. The two outcomes are ``heads'' and ``tails,'' each with
equal probabilities 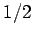 . So,
. So, 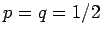 for this system.
for this system.
Suppose that we make  statistically independent observations of
statistically independent observations of 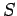 .
Let us determine the probability of
.
Let us determine the probability of 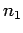 occurrences of the outcome
occurrences of the outcome  and
and 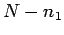 occurrences of the outcome 2, with no regard to the order
of these occurrences. Denote this probability
occurrences of the outcome 2, with no regard to the order
of these occurrences. Denote this probability 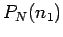 .
This type of calculation crops up again and again
in probability theory. For instance, we might want to know the probability
of getting nine ``heads'' and only one ``tails'' in an experiment where a coin is
tossed ten times, or where ten coins are tossed simultaneously.
.
This type of calculation crops up again and again
in probability theory. For instance, we might want to know the probability
of getting nine ``heads'' and only one ``tails'' in an experiment where a coin is
tossed ten times, or where ten coins are tossed simultaneously.
Consider a simple case in which there are only three observations.
Let us try to evaluate the probability of two occurrences of the outcome 1
and one occurrence of the outcome 2. There are three different ways
of getting this result. We could get the outcome 1 on the first
two observations and the outcome 2 on the third. Or, we could get the outcome
2 on the first observation and the outcome 1 on the latter two observations.
Or, we could get the outcome 1 on the first and last observations and the
outcome 2 on the middle observation. Writing this symbolically
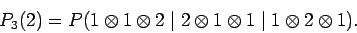 |
(12) |
This formula looks a bit scary, but all we have done here is to
write out symbolically what was just said in words. Where we said ``and''
we have written the symbolic operator 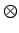 ,
and where we said ``or'' we have written
the symbolic operator
,
and where we said ``or'' we have written
the symbolic operator 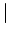 . This symbolic representation is helpful
because of the two basic
rules for combining probabilities which we derived earlier
. This symbolic representation is helpful
because of the two basic
rules for combining probabilities which we derived earlier
The straightforward application of these rules gives
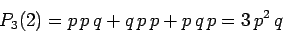 |
(15) |
in the case under consideration.
The
probability of obtaining 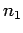 occurrences of the outcome
occurrences of the outcome  in
in
 observations is given by
observations is given by
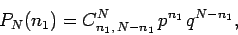 |
(16) |
where
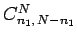 is the number of ways
of arranging two distinct sets of
is the number of ways
of arranging two distinct sets of 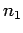 and
and 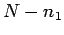 indistinguishable
objects. Hopefully, that this is, at least, plausible from the example we
just discussed. There, the probability of
getting two occurrences of the outcome 1 and one occurrence of the
outcome 2 was obtained by writing out all of the possible arrangements of two
indistinguishable
objects. Hopefully, that this is, at least, plausible from the example we
just discussed. There, the probability of
getting two occurrences of the outcome 1 and one occurrence of the
outcome 2 was obtained by writing out all of the possible arrangements of two
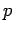 s (the probability of outcome 1) and one
s (the probability of outcome 1) and one 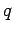 (the probability of
outcome 2), and then added them all together.
(the probability of
outcome 2), and then added them all together.



Next: Combinatorial analysis
Up: Probability theory
Previous: Combining probabilities
Richard Fitzpatrick
2006-02-02
![]() statistically independent observations of
statistically independent observations of ![]() .
Let us determine the probability of
.
Let us determine the probability of ![]() occurrences of the outcome
occurrences of the outcome ![]() and
and ![]() occurrences of the outcome 2, with no regard to the order
of these occurrences. Denote this probability
occurrences of the outcome 2, with no regard to the order
of these occurrences. Denote this probability ![]() .
This type of calculation crops up again and again
in probability theory. For instance, we might want to know the probability
of getting nine ``heads'' and only one ``tails'' in an experiment where a coin is
tossed ten times, or where ten coins are tossed simultaneously.
.
This type of calculation crops up again and again
in probability theory. For instance, we might want to know the probability
of getting nine ``heads'' and only one ``tails'' in an experiment where a coin is
tossed ten times, or where ten coins are tossed simultaneously.
![]() occurrences of the outcome
occurrences of the outcome ![]() in
in
![]() observations is given by
observations is given by