Next: The two-state system
Up: Probability theory
Previous: What is probability?
Consider two distinct possible outcomes, 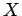 and
and 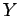 ,
of an observation made on the system
,
of an observation made on the system 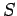 , with probabilities of
occurrence
, with probabilities of
occurrence  and
and
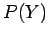 , respectively. Let us determine the probability of
obtaining the outcome
, respectively. Let us determine the probability of
obtaining the outcome 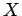 or
or 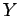 , which we shall denote
, which we shall denote 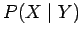 .
From the basic definition of probability
.
From the basic definition of probability
 |
(2) |
where
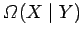 is the number of systems in the ensemble which exhibit
either the outcome
is the number of systems in the ensemble which exhibit
either the outcome 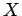 or the outcome
or the outcome 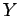 . It is clear that
. It is clear that
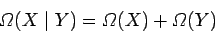 |
(3) |
if the outcomes 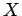 and
and 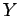 are mutually exclusive (which they must be the case
if they are two distinct outcomes). Thus,
are mutually exclusive (which they must be the case
if they are two distinct outcomes). Thus,
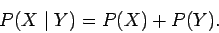 |
(4) |
So, the probability of the outcome 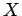 or the outcome
or the outcome 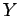 is just the
sum
of the individual probabilities of
is just the
sum
of the individual probabilities of 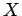 and
and 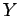 . For instance, with a six
sided die the probability of throwing any particular number (one to six) is
. For instance, with a six
sided die the probability of throwing any particular number (one to six) is
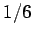 , because all of the possible outcomes are considered to be equally
likely. It follows from what has just been said that the probability of
throwing either a one or a two is simply
, because all of the possible outcomes are considered to be equally
likely. It follows from what has just been said that the probability of
throwing either a one or a two is simply 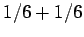 , which equals
, which equals 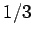 .
.
Let us denote all of the 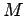 , say, possible outcomes of an observation
made on the system
, say, possible outcomes of an observation
made on the system 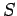 by
by
 , where
, where 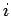 runs from
runs from  to
to 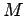 . Let us
determine the probability of obtaining
any of these outcomes. This quantity is clearly unity,
from the basic definition of probability, because every one
of the systems in the ensemble must
exhibit one of the possible outcomes. But, this quantity is also equal to
the sum of the probabilities of all the individual outcomes, by (4),
so we conclude that
this sum is equal to unity. Thus,
. Let us
determine the probability of obtaining
any of these outcomes. This quantity is clearly unity,
from the basic definition of probability, because every one
of the systems in the ensemble must
exhibit one of the possible outcomes. But, this quantity is also equal to
the sum of the probabilities of all the individual outcomes, by (4),
so we conclude that
this sum is equal to unity. Thus,
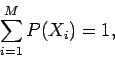 |
(5) |
which is called the normalization condition, and must be satisfied by
any complete set of probabilities. This condition is equivalent to the
self-evident statement that an observation of a system must definitely
result in one of its possible outcomes.
There is another way in which we can combine probabilities. Suppose
that we
make an observation on a state picked at random from the ensemble and then
pick a second state completely independently and
make another observation. We are assuming here that the first
observation does not influence the second observation in
any way. The fancy mathematical way of saying this is that the two
observations are statistically independent.
Let us determine the probability of obtaining
the outcome 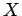 in the first state and
the outcome
in the first state and
the outcome 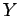 in the second state, which we shall denote
in the second state, which we shall denote
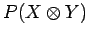 .
In order to determine this probability, we have to form an ensemble of all
of the possible pairs of states which we could choose from the ensemble
.
In order to determine this probability, we have to form an ensemble of all
of the possible pairs of states which we could choose from the ensemble
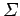 . Let us denote this ensemble
. Let us denote this ensemble
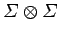 .
It is obvious that the number of pairs of states in this new
ensemble is just the
square of the number of states in the original ensemble, so
.
It is obvious that the number of pairs of states in this new
ensemble is just the
square of the number of states in the original ensemble, so
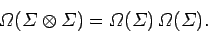 |
(6) |
It is also fairly obvious that the number of pairs of states
in the ensemble
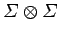 which exhibit the
outcome
which exhibit the
outcome 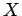 in the first state and
in the first state and 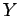 in the second state
is just the
product of the number of states which exhibit the outcome
in the second state
is just the
product of the number of states which exhibit the outcome 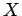 and the number of states which exhibit the outcome
and the number of states which exhibit the outcome 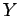 in the original
ensemble, so
in the original
ensemble, so
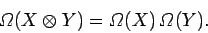 |
(7) |
It follows from the basic definition of probability that
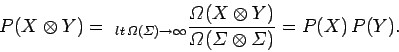 |
(8) |
Thus, the probability of obtaining the outcomes 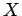 and
and
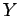 in two statistically independent
observations is just the product of the individual probabilities of
in two statistically independent
observations is just the product of the individual probabilities of
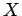 and
and 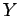 . For instance, the probability of throwing a one and then a two
on a six sided die is
. For instance, the probability of throwing a one and then a two
on a six sided die is
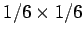 , which equals
, which equals 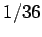 .
.



Next: The two-state system
Up: Probability theory
Previous: What is probability?
Richard Fitzpatrick
2006-02-02


![]() , say, possible outcomes of an observation
made on the system
, say, possible outcomes of an observation
made on the system ![]() by
by
![]() , where
, where ![]() runs from
runs from ![]() to
to ![]() . Let us
determine the probability of obtaining
any of these outcomes. This quantity is clearly unity,
from the basic definition of probability, because every one
of the systems in the ensemble must
exhibit one of the possible outcomes. But, this quantity is also equal to
the sum of the probabilities of all the individual outcomes, by (4),
so we conclude that
this sum is equal to unity. Thus,
. Let us
determine the probability of obtaining
any of these outcomes. This quantity is clearly unity,
from the basic definition of probability, because every one
of the systems in the ensemble must
exhibit one of the possible outcomes. But, this quantity is also equal to
the sum of the probabilities of all the individual outcomes, by (4),
so we conclude that
this sum is equal to unity. Thus,
![]() in the first state and
the outcome
in the first state and
the outcome ![]() in the second state, which we shall denote
in the second state, which we shall denote
![]() .
In order to determine this probability, we have to form an ensemble of all
of the possible pairs of states which we could choose from the ensemble
.
In order to determine this probability, we have to form an ensemble of all
of the possible pairs of states which we could choose from the ensemble
![]() . Let us denote this ensemble
. Let us denote this ensemble
![]() .
It is obvious that the number of pairs of states in this new
ensemble is just the
square of the number of states in the original ensemble, so
.
It is obvious that the number of pairs of states in this new
ensemble is just the
square of the number of states in the original ensemble, so