


Next: Equipartition Theorem
Up: Applications of Statistical Thermodynamics
Previous: Gibb's Paradox
General Paramagnetism
In Section 7.3, we considered the special case of paramagnetism
in which all the atoms that make up the substance under investigation
possess spin 1/2. Let us now discuss the general case.
Consider a system consisting of  non-interacting atoms in a substance
held at absolute temperature
non-interacting atoms in a substance
held at absolute temperature  , and placed in an external magnetic field,
, and placed in an external magnetic field,
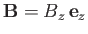 ,
that points in the
,
that points in the  -direction. The magnetic energy of a given atom is written
-direction. The magnetic energy of a given atom is written
where
 is the atom's magnetic moment. Now, the magnetic moment of an atom
is proportional to its total electronic angular momentum,
is the atom's magnetic moment. Now, the magnetic moment of an atom
is proportional to its total electronic angular momentum,
 . In fact,
. In fact,
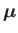 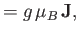 |
(7.92) |
where
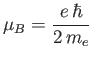 |
(7.93) |
is a standard unit of magnetic moment known as the Bohr magneton. Here, 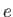 is the magnitude of the electron
charge, and
is the magnitude of the electron
charge, and 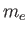 the electron mass. Moreover,
the electron mass. Moreover, 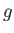 is a dimensionless number of order unity that is called the g-factor
of the atom.
is a dimensionless number of order unity that is called the g-factor
of the atom.
Combining Equations (7.91) and (7.92), we obtain
 |
(7.94) |
Now, according to standard quantum mechanics,
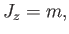 |
(7.95) |
where  is an integer that can take on all values between
is an integer that can take on all values between 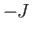 and
and  . Here,
. Here,
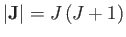 , where
, where  is a positive number that can either take integer or half-integer values. Thus, there are
is a positive number that can either take integer or half-integer values. Thus, there are
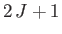 allowed values of
allowed values of  , corresponding to different possible projections of the
angular momentum vector along the
, corresponding to different possible projections of the
angular momentum vector along the 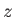 -direction.
It follows from Equation (7.94) that the possible magnetic
energies of an atom are
-direction.
It follows from Equation (7.94) that the possible magnetic
energies of an atom are
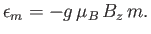 |
(7.96) |
For example, if 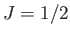 (corresponding to a spin-1/2 system) then there are only
two possible energies, corresponding to
(corresponding to a spin-1/2 system) then there are only
two possible energies, corresponding to 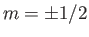 . This was the situation
considered in Section 7.3. (To be more exact, a spin-1/2 system corresponds to
. This was the situation
considered in Section 7.3. (To be more exact, a spin-1/2 system corresponds to 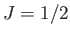 and
and 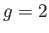 .)
.)
The probability, 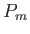 , that an atom is in a state labeled
, that an atom is in a state labeled  is
is
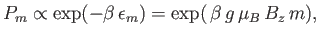 |
(7.97) |
where
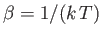 . According to Equation (7.92), the corresponding
. According to Equation (7.92), the corresponding  -component of the magnetic
moment is
-component of the magnetic
moment is
 |
(7.98) |
Hence, the mean  -component of the magnetic moment is
-component of the magnetic moment is
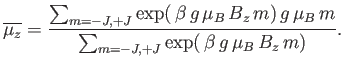 |
(7.99) |
The numerator in the previous expression is conveniently expressed as a derivative with respect to the external parameter 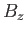 :
:
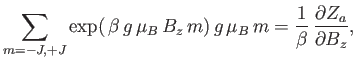 |
(7.100) |
where
 |
(7.101) |
is the partition function of a single atom. Thus, Equation (7.99) becomes
 |
(7.102) |
In order to calculate 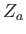 , it is convenient to define
, it is convenient to define
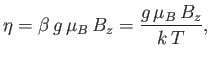 |
(7.103) |
which is a dimensionless parameter that measures the ratio of the magnetic energy,
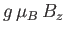 ,
that acts to align the atomic magnetic moments parallel to the external magnetic field, to the thermal energy,
,
that acts to align the atomic magnetic moments parallel to the external magnetic field, to the thermal energy, 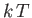 ,
that acts to keep the magnetic moment randomly orientated.
Thus, Equation (7.101) becomes
,
that acts to keep the magnetic moment randomly orientated.
Thus, Equation (7.101) becomes
![$\displaystyle Z_a =\sum_{m=-J,+J}\exp(m \eta)= {\rm e}^{-\eta J}\sum_{k=0,2J}[\exp(\eta)]^{ k}.$](img1455.png) |
(7.104) |
The previous geometric series can be summed to give
![$\displaystyle Z_a = {\rm e}^{-\eta J}\left\{\frac{1-[\exp(\eta)]^{ 2J+1}}{1-\exp(\eta)}\right\}.$](img1456.png) |
(7.105) |
(See Exercise 1.) Multiplying the numerator and denominator by
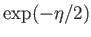 , we
obtain
, we
obtain
![$\displaystyle Z_a = \frac{\exp[-\eta (J+1/2)]+\exp[ \eta (J+1/2)]}{\exp(-\eta/2)-\exp( \eta/2)},$](img1458.png) |
(7.106) |
or
![$\displaystyle Z_a =\frac{\sinh[(J+1/2) \eta]}{\sinh(\eta/2)},$](img1459.png) |
(7.107) |
where the hyperbolic sine is defined
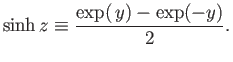 |
(7.108) |
Thus,
![$\displaystyle \ln Z_a =\ln \sinh[(J+1/2) \eta]-\ln\sinh(\eta/2).$](img1461.png) |
(7.109) |
According to Equations (7.102) and (7.103),
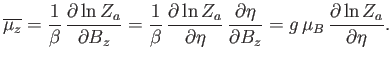 |
(7.110) |
Hence,
![$\displaystyle \overline{\mu_z} = g \mu_B\left\{\frac{(J+1/2) \cosh[(J+1/2) \eta]}{\sinh[(J+1/2) \eta]}-\frac{(1/2) \cosh(\eta/2)}{\sinh(\eta/2)}\right\},$](img1463.png) |
(7.111) |
or
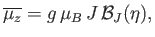 |
(7.112) |
where
![$\displaystyle {\cal B}_J(\eta) =\frac{1}{J}\left\{\left(J+\frac{1}{2}\right)\co...
...c{1}{2}\right)\eta\right]-\frac{1}{2} \coth\left(\frac{\eta}{2}\right)\right\}$](img1465.png) |
(7.113) |
is known as the Brillouin function.
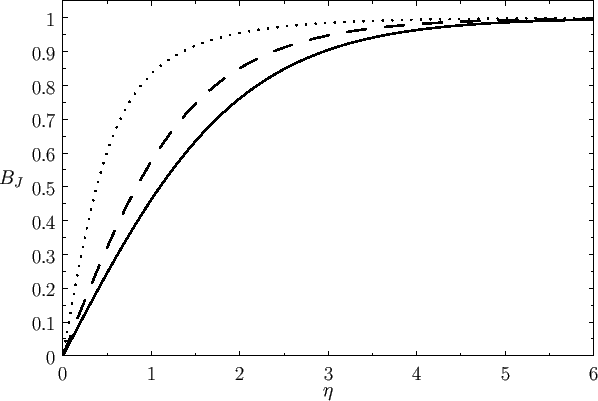
Figure:
The solid, dashed, and dotted curves show the Brillouin function,
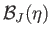 , for
, for 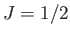 ,
,  , and
, and 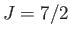 , respectively.
, respectively.
 |
The hyperbolic cotangent is defined
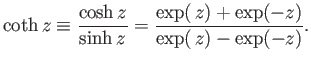 |
(7.114) |
For 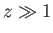 , we have
, we have
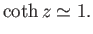 |
(7.115) |
On the other hand, for 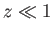 ,
,
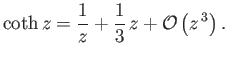 |
(7.116) |
Thus, it follows that
![$\displaystyle {\cal B}_J(\eta)= \frac{1}{J}\left[\left(J+\frac{1}{2}\right)-\frac{1}{2}\right] = 1$](img1472.png) |
(7.117) |
when 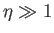 . On the other hand, when
. On the other hand, when 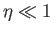 , we get
, we get
which reduces to
 |
(7.119) |
Figure 7.1 shows how
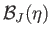 depends on
depends on 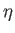 for various values of
for various values of  .
.
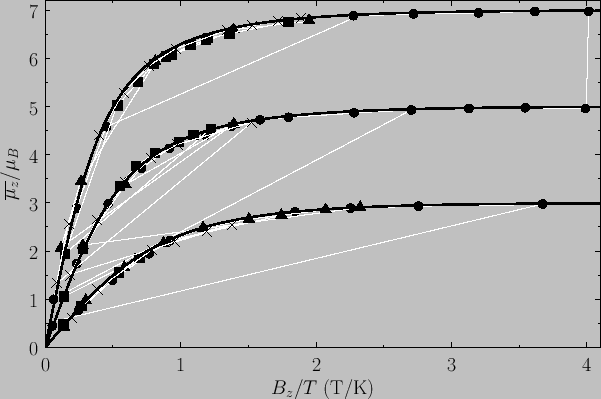
Figure:
The magnetization versus 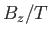 curves
for (lower curve) chromium potassium alum (
curves
for (lower curve) chromium potassium alum (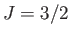 ,
, 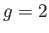 ), (middle curve) iron ammonium alum (
), (middle curve) iron ammonium alum ( ,
, 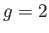 ), and
(top curve) gadolinium sulphate (
), and
(top curve) gadolinium sulphate (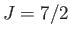 ,
, 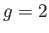 ). The solid lines are the theoretical predictions,
whereas
the data points are experimental measurements. The circles, triangles, crosses, and squares correspond to
). The solid lines are the theoretical predictions,
whereas
the data points are experimental measurements. The circles, triangles, crosses, and squares correspond to
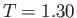 K,
K, 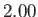 K,
K,  K, and
K, and 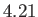 K, respectively. From W.E. Henry, Phys. Rev. 88, 561 (1952).
K, respectively. From W.E. Henry, Phys. Rev. 88, 561 (1952).
 |
If there are  atoms per unit volume then the mean magnetic moment per unit volume (or magnetization) becomes
atoms per unit volume then the mean magnetic moment per unit volume (or magnetization) becomes
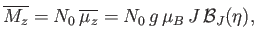 |
(7.120) |
where use has been made of Equation (7.112). If  then Equation (7.119) implies that
then Equation (7.119) implies that
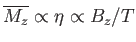 . This relation can be written
. This relation can be written
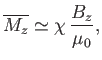 |
(7.121) |
where the dimensionless constant of proportionality,
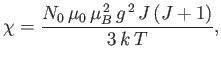 |
(7.122) |
is known as the magnetic susceptibility. Thus,
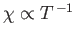 --a result that is called Curie's law. (See Section 7.3.)
If
--a result that is called Curie's law. (See Section 7.3.)
If 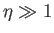 then
then
 |
(7.123) |
This corresponds to magnetic saturation--a situation in which each atom has the maximum component of the magnetic
moment parallel to the magnetic field,
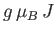 , that it can possibly have.
, that it can possibly have.
Figure 7.2 compares
the experimental and theoretical magnetization versus
field-strength curves for three different paramagnetic substances containing atoms of total angular momentum 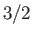 ,
, 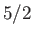 ,
and
,
and  particles, showing excellent agreement between theory and experiment. Note that, in all cases, the magnetization is proportional to the
magnetic field-strength at small field-strengths, but saturates at some
constant value as the field-strength increases.
particles, showing excellent agreement between theory and experiment. Note that, in all cases, the magnetization is proportional to the
magnetic field-strength at small field-strengths, but saturates at some
constant value as the field-strength increases.
The previous analysis completely neglects any interaction between the
spins of neighboring atoms or molecules. It turns out that this is
a fairly good approximation for paramagnetic substances. However, for
ferromagnetic substances, in which the spins of neighboring atoms
interact very strongly, this approximation breaks down completely. (See Section 7.17.) Thus, the
previous analysis does not apply to ferromagnetic substances.



Next: Equipartition Theorem
Up: Applications of Statistical Thermodynamics
Previous: Gibb's Paradox
Richard Fitzpatrick
2016-01-25
![]() non-interacting atoms in a substance
held at absolute temperature
non-interacting atoms in a substance
held at absolute temperature ![]() , and placed in an external magnetic field,
, and placed in an external magnetic field,
![]() ,
that points in the
,
that points in the ![]() -direction. The magnetic energy of a given atom is written
-direction. The magnetic energy of a given atom is written
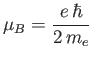
![]() , that an atom is in a state labeled
, that an atom is in a state labeled ![]() is
is
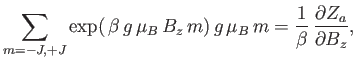
![]() , it is convenient to define
, it is convenient to define
![$\displaystyle Z_a =\sum_{m=-J,+J}\exp(m \eta)= {\rm e}^{-\eta J}\sum_{k=0,2J}[\exp(\eta)]^{ k}.$](img1455.png)
![$\displaystyle Z_a = {\rm e}^{-\eta J}\left\{\frac{1-[\exp(\eta)]^{ 2J+1}}{1-\exp(\eta)}\right\}.$](img1456.png)
![$\displaystyle Z_a = \frac{\exp[-\eta (J+1/2)]+\exp[ \eta (J+1/2)]}{\exp(-\eta/2)-\exp( \eta/2)},$](img1458.png)
![$\displaystyle Z_a =\frac{\sinh[(J+1/2) \eta]}{\sinh(\eta/2)},$](img1459.png)
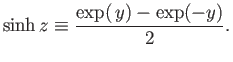
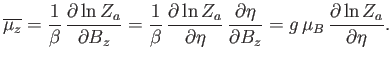
![$\displaystyle \overline{\mu_z} = g \mu_B\left\{\frac{(J+1/2) \cosh[(J+1/2) \eta]}{\sinh[(J+1/2) \eta]}-\frac{(1/2) \cosh(\eta/2)}{\sinh(\eta/2)}\right\},$](img1463.png)

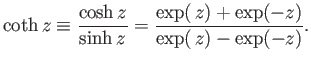
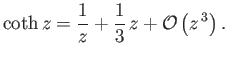
![$\displaystyle =\frac{1}{J}\left\{\left(J+\frac{1}{2}\right)\left[\frac{1}{(J+1/...
...right)\eta\right]-\frac{1}{2}\left(\frac{2}{\eta}+\frac{\eta}{6}\right)\right\}$](img1476.png)
![$\displaystyle =\frac{1}{J}\left[\frac{1}{3}\left(J+\frac{1}{2}\right)^{ 2}\eta...
...} \eta\right]=\frac{\eta}{3 J}\left(J^{ 2}+J+\frac{1}{4}-\frac{1}{4}\right),$](img1477.png)

![]() atoms per unit volume then the mean magnetic moment per unit volume (or magnetization) becomes
atoms per unit volume then the mean magnetic moment per unit volume (or magnetization) becomes
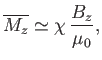
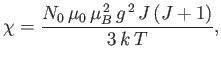
![]() ,
, ![]() ,
and
,
and ![]() particles, showing excellent agreement between theory and experiment. Note that, in all cases, the magnetization is proportional to the
magnetic field-strength at small field-strengths, but saturates at some
constant value as the field-strength increases.
particles, showing excellent agreement between theory and experiment. Note that, in all cases, the magnetization is proportional to the
magnetic field-strength at small field-strengths, but saturates at some
constant value as the field-strength increases.