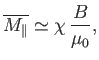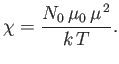Next: System with Specified Mean
Up: Applications of Statistical Thermodynamics
Previous: Canonical Probability Distribution
Spin-1/2 Paramagnetism
The simplest microscopic system that we can analyze using the canonical probability distribution
is one
that has only two possible states. (There would clearly be little point in analyzing
a system with only one possible state.) Most elements, and some compounds, are
paramagnetic. In other words, their constituent atoms, or molecules,
possess a permanent
magnetic moment due to the presence of one or more unpaired electrons. Consider a
substance whose constituent
particles contain only one unpaired electron (with zero orbital angular momentum). Such particles have spin
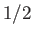 [i.e., their spin angular momentum is
[i.e., their spin angular momentum is
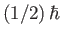 ], and consequently possess an intrinsic magnetic moment,
], and consequently possess an intrinsic magnetic moment,  .
According to quantum mechanics, the magnetic moment of a spin-
.
According to quantum mechanics, the magnetic moment of a spin-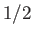 particle
can
point either parallel or antiparallel to an external magnetic field,
particle
can
point either parallel or antiparallel to an external magnetic field, 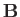 .
Let us determine the mean magnetic moment (parallel
to
.
Let us determine the mean magnetic moment (parallel
to 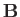 ),
),
 , of the constituent particles of
the substance when its absolute temperature is
, of the constituent particles of
the substance when its absolute temperature is  .
We shall assume, for the sake of simplicity, that each atom (or molecule)
only interacts weakly
with its neighboring atoms. This enables us to focus attention on a single atom, and
to treat the remaining atoms as a heat bath at temperature
.
We shall assume, for the sake of simplicity, that each atom (or molecule)
only interacts weakly
with its neighboring atoms. This enables us to focus attention on a single atom, and
to treat the remaining atoms as a heat bath at temperature  .
.
Our atom can be in one of two possible states. Namely, the 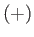 state in which its spin
points up (i.e., parallel to
state in which its spin
points up (i.e., parallel to 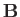 ), or the
), or the 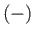 state in which its
spin points down (i.e., antiparallel to
state in which its
spin points down (i.e., antiparallel to 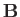 ). In the
). In the 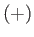 state,
the atomic magnetic moment is parallel to the magnetic field, so that
state,
the atomic magnetic moment is parallel to the magnetic field, so that
 . The magnetic energy of the atom is
. The magnetic energy of the atom is
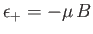 .
In the
.
In the 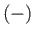 state, the atomic magnetic moment is antiparallel to the magnetic
field, so that
state, the atomic magnetic moment is antiparallel to the magnetic
field, so that
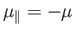 . The magnetic energy of the atom is
. The magnetic energy of the atom is
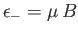 .
.
According to the canonical distribution, the probability of finding the atom
in the 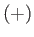 state is
state is
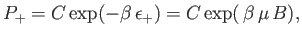 |
(7.13) |
where 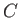 is a constant, and
is a constant, and
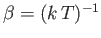 .
Likewise, the probability of finding the atom in the
.
Likewise, the probability of finding the atom in the 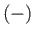 state is
state is
 |
(7.14) |
Clearly, the most probable
state is the state with the lower energy [i.e., the 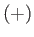 state].
Thus, the mean magnetic moment points in the direction of the magnetic field
(i.e., the atomic spin is more likely to point parallel to the field than antiparallel).
state].
Thus, the mean magnetic moment points in the direction of the magnetic field
(i.e., the atomic spin is more likely to point parallel to the field than antiparallel).
It is apparent that the critical parameter in a paramagnetic system is
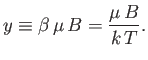 |
(7.15) |
This parameter measures the ratio of the typical magnetic energy of the atom, 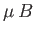 , to
its typical thermal energy,
, to
its typical thermal energy, 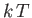 . If the thermal energy greatly exceeds the magnetic
energy then
. If the thermal energy greatly exceeds the magnetic
energy then 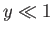 , and the probability that the atomic moment points parallel
to the magnetic field is about the same as the probability that it points
antiparallel. In this situation, we expect the mean atomic moment to
be small, so that
, and the probability that the atomic moment points parallel
to the magnetic field is about the same as the probability that it points
antiparallel. In this situation, we expect the mean atomic moment to
be small, so that
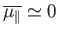 . On the other hand, if the
magnetic energy greatly exceeds the thermal energy then
. On the other hand, if the
magnetic energy greatly exceeds the thermal energy then  , and the atomic
moment is far more likely to be directed parallel to the magnetic field than antiparallel.
In this situation, we expect
, and the atomic
moment is far more likely to be directed parallel to the magnetic field than antiparallel.
In this situation, we expect
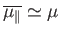 .
.
Let us calculate the mean atomic moment,
 . The usual
definition of a mean value gives
. The usual
definition of a mean value gives
![$\displaystyle \overline{\mu_\parallel} = \frac{ P_{+} \mu + P_{-} (-\mu)}{P...
...p(-\beta \mu B)} { \exp( \beta \mu B)+ \exp(-\beta \mu B)}\right].$](img1316.png) |
(7.16) |
This can also be written
 |
(7.17) |
where the hyperbolic tangent is defined
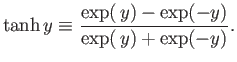 |
(7.18) |
For small arguments, 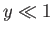 ,
,
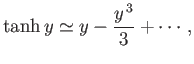 |
(7.19) |
whereas for large arguments,  ,
,
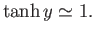 |
(7.20) |
It follows that at comparatively high temperatures,
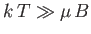 ,
,
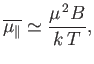 |
(7.21) |
whereas at comparatively low temperatures,
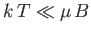 ,
,
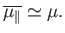 |
(7.22) |
Suppose that the substance contains 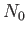 atoms (or molecules) per unit volume.
The magnetization is defined as the mean magnetic moment per unit
volume, and is given by
atoms (or molecules) per unit volume.
The magnetization is defined as the mean magnetic moment per unit
volume, and is given by
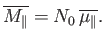 |
(7.23) |
At high temperatures,
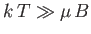 , the mean magnetic moment, and, hence, the
magnetization, is proportional to the applied magnetic field, so we can write
, the mean magnetic moment, and, hence, the
magnetization, is proportional to the applied magnetic field, so we can write
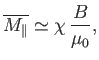 |
(7.24) |
where 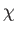 is a dimensionless constant of proportionality known as the
magnetic susceptibility, and
is a dimensionless constant of proportionality known as the
magnetic susceptibility, and  the magnetic permeability of free space.
It is clear that the magnetic susceptibility of a spin-1/2 paramagnetic substance
takes the form
the magnetic permeability of free space.
It is clear that the magnetic susceptibility of a spin-1/2 paramagnetic substance
takes the form
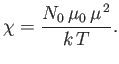 |
(7.25) |
The fact that
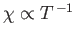 is known as Curie's law, because it
was discovered experimentally by Pierre Curie at the end of the nineteenth century.
At low temperatures,
is known as Curie's law, because it
was discovered experimentally by Pierre Curie at the end of the nineteenth century.
At low temperatures,
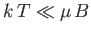 ,
,
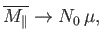 |
(7.26) |
so the magnetization becomes independent of the applied field. This corresponds to
the maximum possible magnetization, in which all atomic moments are aligned
parallel to the field. The breakdown of the
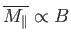 law
at low temperatures (or high magnetic fields) is known as saturation.
law
at low temperatures (or high magnetic fields) is known as saturation.



Next: System with Specified Mean
Up: Applications of Statistical Thermodynamics
Previous: Canonical Probability Distribution
Richard Fitzpatrick
2016-01-25
![]() state in which its spin
points up (i.e., parallel to
state in which its spin
points up (i.e., parallel to ![]() ), or the
), or the ![]() state in which its
spin points down (i.e., antiparallel to
state in which its
spin points down (i.e., antiparallel to ![]() ). In the
). In the ![]() state,
the atomic magnetic moment is parallel to the magnetic field, so that
state,
the atomic magnetic moment is parallel to the magnetic field, so that
![]() . The magnetic energy of the atom is
. The magnetic energy of the atom is
![]() .
In the
.
In the ![]() state, the atomic magnetic moment is antiparallel to the magnetic
field, so that
state, the atomic magnetic moment is antiparallel to the magnetic
field, so that
![]() . The magnetic energy of the atom is
. The magnetic energy of the atom is
![]() .
.
![]() state is
state is
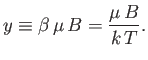
![]() . The usual
definition of a mean value gives
. The usual
definition of a mean value gives
![$\displaystyle \overline{\mu_\parallel} = \frac{ P_{+} \mu + P_{-} (-\mu)}{P...
...p(-\beta \mu B)} { \exp( \beta \mu B)+ \exp(-\beta \mu B)}\right].$](img1316.png)

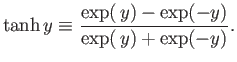
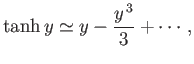
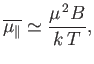
![]() atoms (or molecules) per unit volume.
The magnetization is defined as the mean magnetic moment per unit
volume, and is given by
atoms (or molecules) per unit volume.
The magnetization is defined as the mean magnetic moment per unit
volume, and is given by