


Next: Stability of Single-Phase Substance
Up: Multi-Phase Systems
Previous: Equilibrium of Constant-Temperature System
Equilibrium of Constant-Temperature Constant-Pressure System
Another case of physical interest is that where a system,  , is maintained under conditions of both constant temperature and
constant pressure. This is a situation that occurs frequently in the laboratory, where we might carry out an experiment in a
thermostat at atmospheric pressure (say). Therefore, let us suppose that
, is maintained under conditions of both constant temperature and
constant pressure. This is a situation that occurs frequently in the laboratory, where we might carry out an experiment in a
thermostat at atmospheric pressure (say). Therefore, let us suppose that  is in thermal contact with a heat reservoir,
is in thermal contact with a heat reservoir,  , that is
held at the constant temperature
, that is
held at the constant temperature 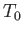 , and at the constant pressure
, and at the constant pressure 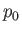 . The system
. The system  can exchange heat with the reservoir,
can exchange heat with the reservoir,  , but
the latter is so large that its temperature,
, but
the latter is so large that its temperature, 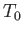 , remains constant. Likewise, the system
, remains constant. Likewise, the system  can change its volume,
can change its volume,  , at the expense of that
of the reservoir,
, at the expense of that
of the reservoir,  , doing work on the reservoir in the process. However,
, doing work on the reservoir in the process. However,  is so large that its pressure,
is so large that its pressure, 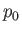 , remains unaffected by
this relatively small volume change.
, remains unaffected by
this relatively small volume change.
The analysis of the equilibrium conditions for system  follows similar lines to the that in the previous section.
The entropy,
follows similar lines to the that in the previous section.
The entropy, 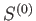 , of the combined system
, of the combined system
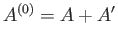 satisfies the condition that in any spontaneous process
satisfies the condition that in any spontaneous process
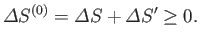 |
(9.19) |
If  absorbs heat
absorbs heat 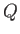 from
from  in this process then
in this process then
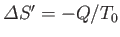 . Furthermore, the first law of
thermodynamics yields
. Furthermore, the first law of
thermodynamics yields
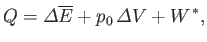 |
(9.20) |
where
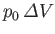 is the work done by
is the work done by  against the constant pressure,
against the constant pressure, 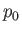 , of the reservoir,
, of the reservoir,  , and where
, and where
 denotes
any other work done by
denotes
any other work done by  in the process. (For example,
in the process. (For example,
 might refer to electrical work.) Thus, we
can write
might refer to electrical work.) Thus, we
can write
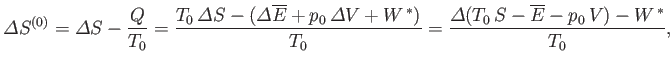 |
(9.21) |
or
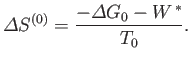 |
(9.22) |
Here, we have made use of the fact that 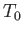 and
and 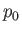 are constants. We have also introduced the definition
are constants. We have also introduced the definition
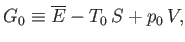 |
(9.23) |
where 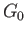 becomes the Gibbs free energy,
becomes the Gibbs free energy,
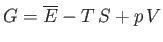 , of system
, of system  when the temperature and
pressure of this system are both equal to those of the reservoir,
when the temperature and
pressure of this system are both equal to those of the reservoir,  .
.
The fundamental condition (9.19) can be combined with Equation (9.22) to give
 |
(9.24) |
(assuming that 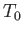 is positive). This relation implies that the maximum work (other than the work done on the pressure reservoir) that
can be done by system
is positive). This relation implies that the maximum work (other than the work done on the pressure reservoir) that
can be done by system  is
is
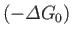 . (Incidentally, this is the reason that
. (Incidentally, this is the reason that 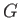 is also called a ``free energy''.)
The maximum work corresponds to the equality sign in the preceding equation, and
is obtained when the process used is quasi-static (so that
is also called a ``free energy''.)
The maximum work corresponds to the equality sign in the preceding equation, and
is obtained when the process used is quasi-static (so that  is always in equilibrium with
is always in equilibrium with  , and
, and 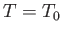 ,
, 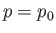 ).
).
If the external parameters of system  (except its volume) are held constant then
(except its volume) are held constant then
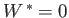 , and Equation (9.24) yields the condition
, and Equation (9.24) yields the condition
 |
(9.25) |
Thus, we arrive at the following statement:
If a system is in contact with a reservoir at constant temperature and pressure then the stable equilibrium state
is such that
The preceding statement can again be phrased in more explicit statistical terms. Suppose that the external parameters of  (except its volume) are fixed, so that
(except its volume) are fixed, so that
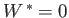 . Furthermore, let
. Furthermore, let  be described by some parameter
be described by some parameter  . If
. If  changes from some standard value
changes from some standard value 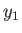 then
the corresponding change in the total entropy of
then
the corresponding change in the total entropy of 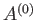 is
is
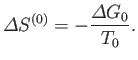 |
(9.26) |
But, in an equilibrium state, the probability,  , that the parameter lies between
, that the parameter lies between  and
and
 is given by
is given by
![$\displaystyle P(y)\propto \exp\left[\frac{S^{(0)}(y)}{k}\right].$](img2649.png) |
(9.27) |
Now, from Equation (9.26),
![$\displaystyle S^{(0)}(y) = S^{(0)}(y_1)-\frac{{\mit\Delta}G_0}{T_0} = S^{(0)}(y_1) - \left[\frac{G_0(y)-G_0(y_1)}{T_0}\right].$](img2650.png) |
(9.28) |
However, because 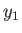 is just some arbitrary constant, the corresponding constant terms can be absorbed into the constant of
proportionality in Equation (9.27), which then becomes
is just some arbitrary constant, the corresponding constant terms can be absorbed into the constant of
proportionality in Equation (9.27), which then becomes
![$\displaystyle P(y)\propto \exp\left[-\frac{G_0(y)}{k T_0}\right].$](img2651.png) |
(9.29) |
This equation shows explicitly that the most probable state is one in which 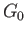 attains a minimum value, and also allows us to determine the relative probability of fluctuations about this state.
attains a minimum value, and also allows us to determine the relative probability of fluctuations about this state.



Next: Stability of Single-Phase Substance
Up: Multi-Phase Systems
Previous: Equilibrium of Constant-Temperature System
Richard Fitzpatrick
2016-01-25
![]() follows similar lines to the that in the previous section.
The entropy,
follows similar lines to the that in the previous section.
The entropy, ![]() , of the combined system
, of the combined system
![]() satisfies the condition that in any spontaneous process
satisfies the condition that in any spontaneous process
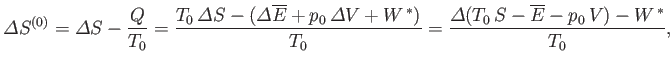
![]() (except its volume) are held constant then
(except its volume) are held constant then
![]() , and Equation (9.24) yields the condition
, and Equation (9.24) yields the condition
![]() (except its volume) are fixed, so that
(except its volume) are fixed, so that
![]() . Furthermore, let
. Furthermore, let ![]() be described by some parameter
be described by some parameter ![]() . If
. If ![]() changes from some standard value
changes from some standard value ![]() then
the corresponding change in the total entropy of
then
the corresponding change in the total entropy of ![]() is
is
![$\displaystyle S^{(0)}(y) = S^{(0)}(y_1)-\frac{{\mit\Delta}G_0}{T_0} = S^{(0)}(y_1) - \left[\frac{G_0(y)-G_0(y_1)}{T_0}\right].$](img2650.png)