

Next: Representation of Waves via
Up: Wave-Particle Duality
Previous: Wavefunctions
As we have just seen, a wave of amplitude 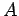 , wavenumber
, wavenumber 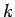 , angular frequency
, angular frequency 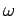 , and phase
angle
, and phase
angle 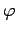 ,
propagating in the positive
,
propagating in the positive  -direction, is represented by the following wavefunction:
-direction, is represented by the following wavefunction:
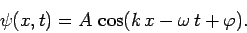 |
(29) |
Now, the type of wave represented above is conventionally termed a one-dimensional plane wave. It is one-dimensional
because its associated wavefunction only depends on the single Cartesian coordinate  .
Furthermore, it is a plane wave because the wave maxima, which are located at
.
Furthermore, it is a plane wave because the wave maxima, which are located at
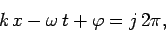 |
(30) |
where 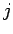 is an integer, consist of a series of parallel planes, normal to the
is an integer, consist of a series of parallel planes, normal to the  -axis, which are equally spaced a distance
-axis, which are equally spaced a distance
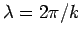 apart, and propagate along the
positive
apart, and propagate along the
positive  -axis at the velocity
-axis at the velocity 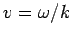 .
These conclusions follow because Eq. (30) can be re-written in the form
.
These conclusions follow because Eq. (30) can be re-written in the form
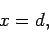 |
(31) |
where
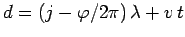 . Moreover, as is well-known, (31)
is the equation of a plane, normal to the
. Moreover, as is well-known, (31)
is the equation of a plane, normal to the  -axis, whose distance of closest approach to the
origin is
-axis, whose distance of closest approach to the
origin is 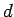 .
.
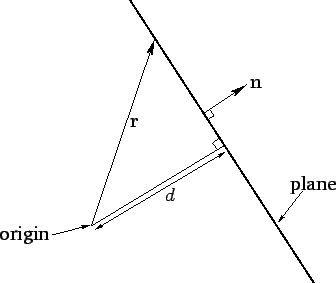
Figure 1:
The solution of
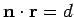 is a plane.
is a plane.
 |
The previous equation can also be written in the coordinate-free form
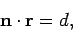 |
(32) |
where
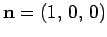 is a unit
vector directed along the positive
is a unit
vector directed along the positive  -axis, and
-axis, and
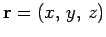 represents the vector displacement of a general point from the origin. Since there is nothing special about the
represents the vector displacement of a general point from the origin. Since there is nothing special about the  -direction, it follows that if
-direction, it follows that if 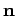 is re-interpreted as a
unit vector pointing in an arbitrary direction then (32) can be re-interpreted as the general equation of a plane.
As before, the plane is normal to
is re-interpreted as a
unit vector pointing in an arbitrary direction then (32) can be re-interpreted as the general equation of a plane.
As before, the plane is normal to
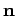 , and its distance of closest approach to the origin is
, and its distance of closest approach to the origin is 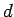 . See Fig. 1. This observation allows us to write the three-dimensional
equivalent to the wavefunction (29) as
. See Fig. 1. This observation allows us to write the three-dimensional
equivalent to the wavefunction (29) as
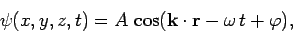 |
(33) |
where the constant vector
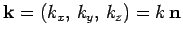 is called the wavevector. The wave represented above is conventionally termed
a three-dimensional plane wave. It is three-dimensional because its wavefunction,
is called the wavevector. The wave represented above is conventionally termed
a three-dimensional plane wave. It is three-dimensional because its wavefunction, 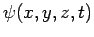 , depends on all
three Cartesian coordinates. Moreover, it is a plane wave because the wave maxima are located at
, depends on all
three Cartesian coordinates. Moreover, it is a plane wave because the wave maxima are located at
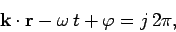 |
(34) |
or
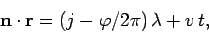 |
(35) |
where
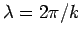 , and
, and 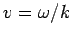 . Note that the wavenumber,
. Note that the wavenumber, 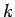 , is the
magnitude of the wavevector,
, is the
magnitude of the wavevector, 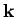 : i.e.,
: i.e.,
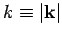 .
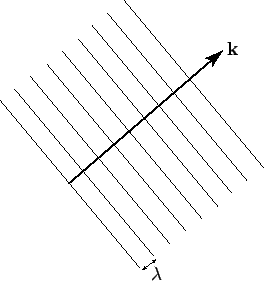
It follows, by comparison with Eq. (32), that the
wave maxima consist of a series of parallel planes, normal to the wavevector, which are equally spaced a distance
.
It follows, by comparison with Eq. (32), that the
wave maxima consist of a series of parallel planes, normal to the wavevector, which are equally spaced a distance 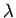 apart, and which propagate in the
apart, and which propagate in the 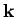 -direction at the velocity
-direction at the velocity 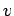 . See Fig. 2. Hence, the direction of the wavevector specifies the wave propagation direction, whereas its magnitude determines the wavenumber,
. See Fig. 2. Hence, the direction of the wavevector specifies the wave propagation direction, whereas its magnitude determines the wavenumber, 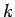 , and, thus, the wavelength,
, and, thus, the wavelength,
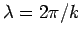 .
.
Figure 2:
Wave maxima associated with a three-dimensional plane wave.
 |


Next: Representation of Waves via
Up: Wave-Particle Duality
Previous: Wavefunctions
Richard Fitzpatrick
2010-07-20