


Next: Plane Waves
Up: Wave-Particle Duality
Previous: Introduction
A wave is defined as a disturbance in some physical system which is periodic in both space and time.
In one dimension, a wave is generally represented in terms of a wavefunction: e.g.,
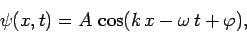 |
(27) |
where  represents position,
represents position,  represents time, and
represents time, and  ,
,  ,
, 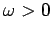 .
For instance, if we are considering a sound wave then
.
For instance, if we are considering a sound wave then 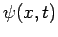 might correspond to the pressure perturbation
associated with the wave at position
might correspond to the pressure perturbation
associated with the wave at position  and time
and time  . On the other hand, if we are considering a light wave then
. On the other hand, if we are considering a light wave then 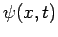 might represent the wave's transverse electric field. As is well-known, the cosine function,
might represent the wave's transverse electric field. As is well-known, the cosine function,  ,
is periodic in its argument,
,
is periodic in its argument,  , with period
, with period 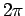 : i.e.,
: i.e.,
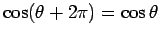 for all
for all  .
The function also oscillates between the minimum and maximum values
.
The function also oscillates between the minimum and maximum values  and
and 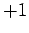 , respectively, as
, respectively, as
 varies. It follows that the wavefunction (27) is periodic in
varies. It follows that the wavefunction (27) is periodic in  with period
with period
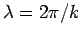 :
i.e.,
:
i.e.,
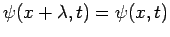 for all
for all  and
and  . Moreover, the wavefunction is periodic
in
. Moreover, the wavefunction is periodic
in  with period
with period 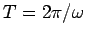 : i.e.,
: i.e.,
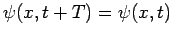 for all
for all  and
and  .
Finally, the wavefunction oscillates between the minimum and
maximum values
.
Finally, the wavefunction oscillates between the minimum and
maximum values 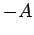 and
and 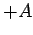 , respectively, as
, respectively, as  and
and  vary. The spatial period of the wave,
vary. The spatial period of the wave,  , is
known as its wavelength, and the temporal period,
, is
known as its wavelength, and the temporal period, 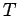 , is called its period. Furthermore, the quantity
, is called its period. Furthermore, the quantity
 is termed the wave amplitude, the quantity
is termed the wave amplitude, the quantity  the wavenumber, and the
quantity
the wavenumber, and the
quantity  the wave angular frequency. Note that the units of
the wave angular frequency. Note that the units of  are radians per second.
The conventional wave frequency, in cycles per second (otherwise known as hertz), is
are radians per second.
The conventional wave frequency, in cycles per second (otherwise known as hertz), is
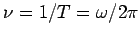 . Finally, the quantity
. Finally, the quantity 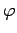 , appearing in expression (27), is termed the
phase angle, and determines the exact positions of the wave maxima and minima at a given time. In fact, the maxima are located at
, appearing in expression (27), is termed the
phase angle, and determines the exact positions of the wave maxima and minima at a given time. In fact, the maxima are located at
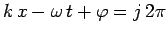 , where
, where 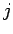 is an integer. This follows
because the maxima of
is an integer. This follows
because the maxima of  occur at
occur at
 . Note that a given maximum
satisfies
. Note that a given maximum
satisfies
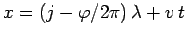 , where
, where 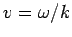 . It follows that the maximum, and, by implication, the whole wave, propagates in
the positive
. It follows that the maximum, and, by implication, the whole wave, propagates in
the positive  -direction at the velocity
-direction at the velocity 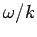 . Analogous reasoning reveals that
. Analogous reasoning reveals that
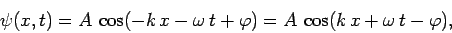 |
(28) |
is the wavefunction of a wave of amplitude  , wavenumber
, wavenumber  , angular frequency
, angular frequency  , and phase
angle
, and phase
angle 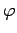 , which propagates in the negative
, which propagates in the negative  -direction at the velocity
-direction at the velocity 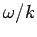 .
.



Next: Plane Waves
Up: Wave-Particle Duality
Previous: Introduction
Richard Fitzpatrick
2010-07-20