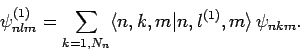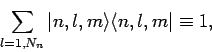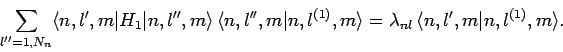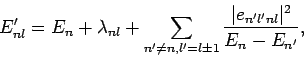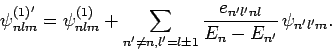Next: Linear Stark Effect
Up: Time-Independent Perturbation Theory
Previous: Quadratic Stark Effect
Degenerate Perturbation Theory
Let us, rather naively, investigate the Stark effect in an excited (i.e.,
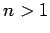 ) state of the hydrogen atom using standard non-degenerate
perturbation theory. We can write
) state of the hydrogen atom using standard non-degenerate
perturbation theory. We can write
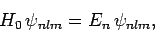 |
(940) |
since the energy eigenstates of the unperturbed Hamiltonian only depend
on the quantum number 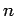 . Making use of the selection rules
(917) and (927), non-degenerate perturbation theory
yields the following expressions for the perturbed energy levels
and eigenstates [see Eqs. (909) and (910)]:
. Making use of the selection rules
(917) and (927), non-degenerate perturbation theory
yields the following expressions for the perturbed energy levels
and eigenstates [see Eqs. (909) and (910)]:
 |
(941) |
and
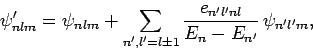 |
(942) |
where
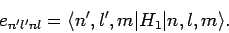 |
(943) |
Unfortunately, if 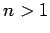 then the summations in the above expressions
are not well-defined, because there exist non-zero matrix elements,
then the summations in the above expressions
are not well-defined, because there exist non-zero matrix elements, 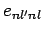 , which couple degenerate eigenstates: i.e., there exist non-zero matrix elements which couple states with the same value of
, which couple degenerate eigenstates: i.e., there exist non-zero matrix elements which couple states with the same value of 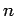 , but
different values of
, but
different values of 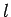 . These particular matrix elements give rise to
singular factors
. These particular matrix elements give rise to
singular factors 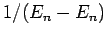 in the summations. This does not occur if
in the summations. This does not occur if
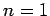 because, in this case, the selection rule
because, in this case, the selection rule 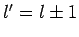 , and the
fact that
, and the
fact that 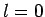 (since
(since 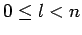 ), only allow
), only allow 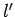 to take the single value 1.
Of course, there is no
to take the single value 1.
Of course, there is no 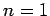 state with
state with 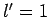 .
Hence, there is only one coupled state corresponding to the
eigenvalue
.
Hence, there is only one coupled state corresponding to the
eigenvalue  . Unfortunately, if
. Unfortunately, if 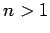 then there are multiple
coupled states corresponding to the eigenvalue
then there are multiple
coupled states corresponding to the eigenvalue 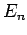 .
.
Note that our problem would disappear if the matrix elements of the
perturbed Hamiltonian corresponding to the same value of 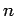 , but
different values of
, but
different values of 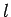 , were all zero: i.e., if
, were all zero: i.e., if
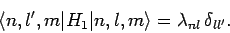 |
(944) |
In this case, all of the singular
terms in Eqs. (941) and (942) would reduce to zero.
Unfortunately, the above equation is not satisfied. Fortunately, we can
always redefine the unperturbed eigenstates corresponding to the
eigenvalue 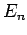 in such a manner that Eq. (944) is satisfied.
Suppose that there are
in such a manner that Eq. (944) is satisfied.
Suppose that there are 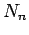 coupled eigenstates belonging
to the eigenvalue
coupled eigenstates belonging
to the eigenvalue 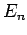 . Let us define
. Let us define 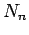 new states
which are linear combinations of our
new states
which are linear combinations of our 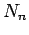 original degenerate eigenstates:
original degenerate eigenstates:
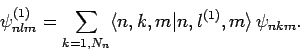 |
(945) |
Note that these new states are also degenerate energy eigenstates of the
unperturbed Hamiltonian, 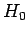 , corresponding to the eigenvalue
, corresponding to the eigenvalue 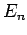 . The
. The
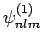 are chosen in such a manner that they are also
eigenstates of the perturbing Hamiltonian,
are chosen in such a manner that they are also
eigenstates of the perturbing Hamiltonian, 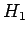 :
i.e., they are simultaneous eigenstates of
:
i.e., they are simultaneous eigenstates of 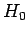 and
and 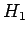 . Thus,
. Thus,
 |
(946) |
The
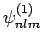 are also chosen so as to be orthonormal:
i.e.,
are also chosen so as to be orthonormal:
i.e.,
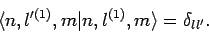 |
(947) |
It follows that
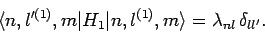 |
(948) |
Thus, if we use the new eigenstates, instead of the old ones, then we
can employ Eqs. (941) and (942) directly, since all
of the singular terms vanish. The only remaining difficulty
is to determine the new eigenstates in terms of the original ones.
Now [see Eq. (874)]
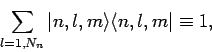 |
(949) |
where 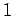 denotes the identity operator in the sub-space of all coupled unperturbed
eigenstates corresponding to the eigenvalue
denotes the identity operator in the sub-space of all coupled unperturbed
eigenstates corresponding to the eigenvalue 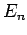 . Using this completeness
relation, the eigenvalue equation (946) can be
transformed into a straightforward matrix equation:
. Using this completeness
relation, the eigenvalue equation (946) can be
transformed into a straightforward matrix equation:
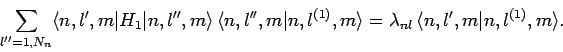 |
(950) |
This can be written more transparently as
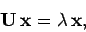 |
(951) |
where the elements of the 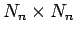 Hermitian matrix
Hermitian matrix  are
are
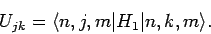 |
(952) |
Provided that the determinant of  is non-zero, Eq. (951)
can always be solved to give
is non-zero, Eq. (951)
can always be solved to give 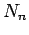 eigenvalues
eigenvalues 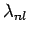 (for
(for 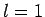 to
to 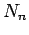 ), with
), with 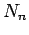 corresponding eigenvectors
corresponding eigenvectors 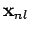 . The
normalized eigenvectors specify the weights of the new eigenstates in terms of the
original eigenstates: i.e.,
. The
normalized eigenvectors specify the weights of the new eigenstates in terms of the
original eigenstates: i.e.,
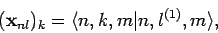 |
(953) |
for 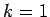 to
to 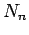 . In our new scheme, Eqs. (941) and (942) yield
. In our new scheme, Eqs. (941) and (942) yield
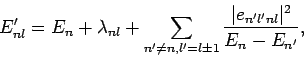 |
(954) |
and
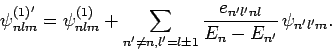 |
(955) |
There are no singular terms in these expressions, since the summations
are over 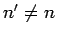 : i.e., they specifically exclude the problematic,
degenerate, unperturbed energy eigenstates corresponding to the eigenvalue
: i.e., they specifically exclude the problematic,
degenerate, unperturbed energy eigenstates corresponding to the eigenvalue
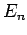 . Note that the first-order energy shifts are equivalent to the
eigenvalues of the matrix equation (951).
. Note that the first-order energy shifts are equivalent to the
eigenvalues of the matrix equation (951).



Next: Linear Stark Effect
Up: Time-Independent Perturbation Theory
Previous: Quadratic Stark Effect
Richard Fitzpatrick
2010-07-20
![]() , but
different values of
, but
different values of ![]() , were all zero: i.e., if
, were all zero: i.e., if