


Next: Ehrenfest Theorem
Up: Quantum Dynamics
Previous: Schrödinger Equation of Motion
Heisenberg Equation of Motion
We have seen that in the Schrödinger scheme the dynamical variables of the
system remain fixed during a period of undisturbed motion, whereas the state kets
evolve according to Equation (229). However, this is not the only way in which
to represent the time evolution of the system.
Suppose that a general state ket  is subject to the transformation
is subject to the transformation
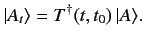 |
(235) |
This is a time-dependent transformation, because the operator 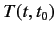 obviously
depends on time. The subscript
obviously
depends on time. The subscript 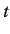 is used to remind us that the transformation
is time-dependent.
The time evolution of the transformed state ket is given by
is used to remind us that the transformation
is time-dependent.
The time evolution of the transformed state ket is given by
 |
(236) |
where use has been made of Equations (222), (224), and the fact that
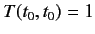 .
Clearly, the transformed state ket does not evolve in time. Thus, the
transformation (235) has the effect of bringing all kets representing
states of undisturbed motion of the system to rest.
.
Clearly, the transformed state ket does not evolve in time. Thus, the
transformation (235) has the effect of bringing all kets representing
states of undisturbed motion of the system to rest.
The transformation must also be applied to bras. The dual of Equation (235)
yields
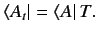 |
(237) |
The transformation rule for a general observable 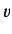 is obtained from the requirement
that the expectation value
is obtained from the requirement
that the expectation value
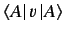 should remain invariant. It is easily
seen that
should remain invariant. It is easily
seen that
 |
(238) |
Thus, a dynamical variable, which corresponds to a fixed linear operator in
Schrödinger's scheme, corresponds to a moving linear operator in this
new scheme. It is clear that the transformation (235) leads us to a scenario
in which the state of the system is represented by
a
fixed vector, and the dynamical variables
are represented by moving linear operators. This is termed the Heisenberg
picture, as opposed to the Schrödinger picture,
which is outlined in Section 3.1.
Consider a dynamical variable 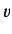 corresponding to a fixed linear operator in
the Schrödinger picture. According to Equation (238), we can write
corresponding to a fixed linear operator in
the Schrödinger picture. According to Equation (238), we can write
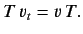 |
(239) |
Differentiation with respect to time yields
 |
(240) |
With the help of Equation (233), this reduces to
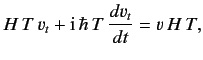 |
(241) |
or
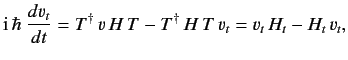 |
(242) |
where
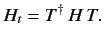 |
(243) |
Equation (242)
can be written
![$\displaystyle {\rm i}\,\hbar\ \frac{d v_t}{dt} = [v_t, H_t].$](img573.png) |
(244) |
Equation (244) shows how the dynamical variables of the system evolve in the
Heisenberg picture. It is denoted the Heisenberg equation of motion.
Note that the time-varying dynamical variables in the Heisenberg picture
are usually called Heisenberg dynamical variables to distinguish them
from Schrödinger dynamical variables (i.e., the corresponding variables in
the Schrödinger picture), which do not evolve in time.
According to Equation (113), the Heisenberg equation of motion can be written
![$\displaystyle \frac{dv_t}{dt} = [v_t, H_t]_{qm},$](img574.png) |
(245) |
where
![$ [\cdots]_{qm}$](img575.png) denotes the quantum Poisson bracket.
Let us compare this equation
with the classical time evolution
equation for a general dynamical variable
denotes the quantum Poisson bracket.
Let us compare this equation
with the classical time evolution
equation for a general dynamical variable 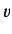 , which can be written
in the form [see Equation (98)]
, which can be written
in the form [see Equation (98)]
![$\displaystyle \frac{dv}{dt} = [v,H]_{cl}.$](img576.png) |
(246) |
Here,
![$ [\cdots]_{cl}$](img577.png) is the classical Poisson bracket, and
is the classical Poisson bracket, and 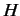 denotes
the classical Hamiltonian. The strong resemblance between
Equations (245) and (246)
provides us with further justification for our identification
of the linear operator
denotes
the classical Hamiltonian. The strong resemblance between
Equations (245) and (246)
provides us with further justification for our identification
of the linear operator 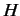 with the energy of the system in quantum mechanics.
with the energy of the system in quantum mechanics.
Note that if the Hamiltonian does not explicitly depend on time (i.e., the system is
not subject to some time-dependent external force) then Equation (234) yields
![$\displaystyle T(t, t_0) = \exp\left[-{\rm i}\, H\,(t-t_0)/\hbar \right].$](img578.png) |
(247) |
This operator manifestly commutes with 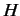 , so
, so
 |
(248) |
Furthermore, Equation (244) gives
![$\displaystyle {\rm i}\,\hbar \,\frac{dH}{dt} = [H, H] = 0.$](img580.png) |
(249) |
Thus, if the energy of the system has no explicit time-dependence then it is
represented by the same non-time-varying operator 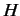 in both the Schrödinger
and Heisenberg pictures.
in both the Schrödinger
and Heisenberg pictures.
Suppose that 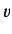 is an observable that commutes with the Hamiltonian
(and, hence, with the time evolution operator
is an observable that commutes with the Hamiltonian
(and, hence, with the time evolution operator 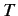 ). It follows from Equation (238)
that
). It follows from Equation (238)
that 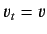 . Heisenberg's equation of motion yields
. Heisenberg's equation of motion yields
![$\displaystyle {\rm i}\,\hbar \,\frac{d v}{dt} = [v, H] = 0.$](img582.png) |
(250) |
Thus, any observable that commutes with the Hamiltonian is a constant
of the motion (hence, it is represented by the same fixed operator in
both the Schrödinger and Heisenberg pictures). Only those observables
that do not commute with the Hamiltonian evolve
in time in the Heisenberg picture.



Next: Ehrenfest Theorem
Up: Quantum Dynamics
Previous: Schrödinger Equation of Motion
Richard Fitzpatrick
2013-04-08
![]() is subject to the transformation
is subject to the transformation
![]() corresponding to a fixed linear operator in
the Schrödinger picture. According to Equation (238), we can write
corresponding to a fixed linear operator in
the Schrödinger picture. According to Equation (238), we can write

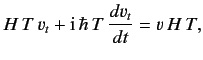
![$\displaystyle {\rm i}\,\hbar \,\frac{dH}{dt} = [H, H] = 0.$](img580.png)
![]() is an observable that commutes with the Hamiltonian
(and, hence, with the time evolution operator
is an observable that commutes with the Hamiltonian
(and, hence, with the time evolution operator ![]() ). It follows from Equation (238)
that
). It follows from Equation (238)
that ![]() . Heisenberg's equation of motion yields
. Heisenberg's equation of motion yields
![$\displaystyle {\rm i}\,\hbar \,\frac{d v}{dt} = [v, H] = 0.$](img582.png)