


Next: Helium Atom
Up: Identical Particles
Previous: Spin Statistics Theorem
Two-Electron System
Consider a system consisting of two electrons. Let 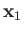 and
and 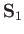 represent the position and spin operators of the first electron, respectively,
and let
represent the position and spin operators of the first electron, respectively,
and let 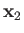 and
and 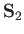 represent the corresponding operators of the second electron. Furthermore,
let
represent the corresponding operators of the second electron. Furthermore,
let
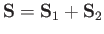 represent the total spin operator of the system. Suppose that the Hamiltonian commutes with
represent the total spin operator of the system. Suppose that the Hamiltonian commutes with  , as is often the case.
It follows that the state of the system is specified by the position eigenvalues
, as is often the case.
It follows that the state of the system is specified by the position eigenvalues
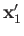 and
and
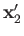 , as well as the total spin
quantum numbers
, as well as the total spin
quantum numbers 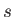 and
and  . As usual, the eigenvalue of
. As usual, the eigenvalue of  is
is
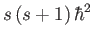 , and the eigenvalue of
, and the eigenvalue of  is
is 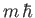 . (See Chapter 5.)
Moreover,
. (See Chapter 5.)
Moreover,  can only take the values
can only take the values 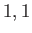 or
or 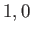 or
or 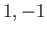 or
or  , respectively. (See Chapter 6.)
The overall wavefunction of the system can be written
, respectively. (See Chapter 6.)
The overall wavefunction of the system can be written
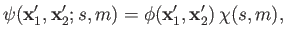 |
(9.44) |
where
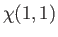 |
 |
(9.45) |
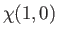 |
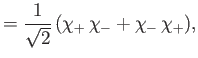 |
(9.46) |
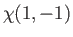 |
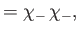 |
(9.47) |
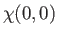 |
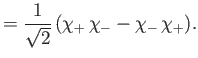 |
(9.48) |
(See Section 6.4.)
Here, the spinor
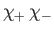 denotes a state in which
denotes a state in which 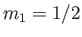 and
and  , et cetera, where
, et cetera, where
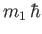 and
and
 are the eigenvalues
of
are the eigenvalues
of  and
and 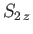 , respectively. The three
, respectively. The three  spinors are usually referred to as triplet spinors, whereas the single
spinors are usually referred to as triplet spinors, whereas the single
 spinor is called the singlet spinor. Note that the triplet spinors are all symmetric with respect to exchange of particles, whereas the
singlet spinor is antisymmetric.
spinor is called the singlet spinor. Note that the triplet spinors are all symmetric with respect to exchange of particles, whereas the
singlet spinor is antisymmetric.
Fermi-Dirac statistics requires that the overall wavefunction be antisymmetric with respect to exchange of particles. Now, according to Equation (9.44),
the overall wavefunction can be written as a product of a spatial wavefunction and a spinor. Moreover, when the system is in the spin-triplet
state (i.e.,  ), the spinor is symmetric with respect to exchange of particles. On the other hand, when the system is in the spin-singlet
state (i.e.,
), the spinor is symmetric with respect to exchange of particles. On the other hand, when the system is in the spin-singlet
state (i.e.,  ), the spinor is antisymmetric. It follows that, to maintain the overall antisymmetry
of the wavefunction, the triplet spatial wavefunction must be antisymmetric with respect to exchange of particles, whereas the singlet
spatial wavefunction must be symmetric. In other words, in the spin-triplet state the spatial wavefunction takes the form
), the spinor is antisymmetric. It follows that, to maintain the overall antisymmetry
of the wavefunction, the triplet spatial wavefunction must be antisymmetric with respect to exchange of particles, whereas the singlet
spatial wavefunction must be symmetric. In other words, in the spin-triplet state the spatial wavefunction takes the form
![$\displaystyle \phi({\bf x}_1,{\bf x}_2) = \frac{1}{\sqrt{2}}\left[\omega_A({\bf x}_1)\,\omega_B({\bf x}_2)-\omega_B({\bf x}_1)\,\omega_A({\bf x}_2)\right],$](img3094.png) |
(9.49) |
whereas in the spin-singlet state the spatial wavefunction is written
![$\displaystyle \phi({\bf x}_1,{\bf x}_2) = \frac{1}{\sqrt{2}}\left[\omega_A({\bf x}_1)\,\omega_B({\bf x}_2)+\omega_B({\bf x}_1)\,\omega_A({\bf x}_2)\right].$](img3095.png) |
(9.50) |
The probability of observing one electron in the volume element
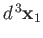 around position
around position 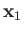 , and the
other in the volume element
, and the
other in the volume element
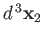 around position
around position 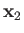 , is proportional to
, is proportional to
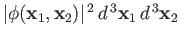 , or
, or
Here, the plus sign corresponds to the spin-singlet state, whereas the minus sign corresponds to the spin-triplet state. We can immediately see that, in the
spin-triplet state, the probability of finding the two electrons at the same point in space is zero. In other words, the two electrons have
a tendency to avoid one another in this state. On the other hand, in the spin-singlet state, there is an enhanced probability of finding the
two electrons at the same point in space (because of the final term in the previous expression). In other words, the two electrons are attracted to
one another in this state.
Note, however, that the spatial probability distributions
associated with the singlet and triplet states differ substantially only when the two single-particle spatial wavefunctions,
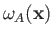 and
and
 ,
overlap: that is, when there exists a region of space in which the two wavefunctions are simultaneously non-negligible.
,
overlap: that is, when there exists a region of space in which the two wavefunctions are simultaneously non-negligible.



Next: Helium Atom
Up: Identical Particles
Previous: Spin Statistics Theorem
Richard Fitzpatrick
2016-01-22
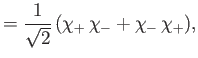
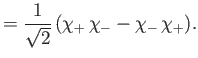
![]() ), the spinor is symmetric with respect to exchange of particles. On the other hand, when the system is in the spin-singlet
state (i.e.,
), the spinor is symmetric with respect to exchange of particles. On the other hand, when the system is in the spin-singlet
state (i.e., ![]() ), the spinor is antisymmetric. It follows that, to maintain the overall antisymmetry
of the wavefunction, the triplet spatial wavefunction must be antisymmetric with respect to exchange of particles, whereas the singlet
spatial wavefunction must be symmetric. In other words, in the spin-triplet state the spatial wavefunction takes the form
), the spinor is antisymmetric. It follows that, to maintain the overall antisymmetry
of the wavefunction, the triplet spatial wavefunction must be antisymmetric with respect to exchange of particles, whereas the singlet
spatial wavefunction must be symmetric. In other words, in the spin-triplet state the spatial wavefunction takes the form
![$\displaystyle \phi({\bf x}_1,{\bf x}_2) = \frac{1}{\sqrt{2}}\left[\omega_A({\bf x}_1)\,\omega_B({\bf x}_2)-\omega_B({\bf x}_1)\,\omega_A({\bf x}_2)\right],$](img3094.png)
![$\displaystyle \phi({\bf x}_1,{\bf x}_2) = \frac{1}{\sqrt{2}}\left[\omega_A({\bf x}_1)\,\omega_B({\bf x}_2)+\omega_B({\bf x}_1)\,\omega_A({\bf x}_2)\right].$](img3095.png)
![\begin{multline}
\frac{1}{2}\left(\vert\omega_A({\bf x}_1)\vert^{\,2}\,\vert\ome...
...ast}({\bf x}_1)\right]\right)d^{\,3} {\bf x}_1\,d^{\,3}{\bf x}_2.
\end{multline}](img3099.png)