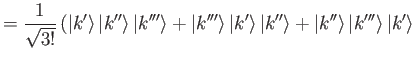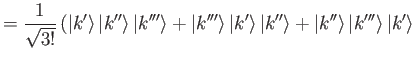Next: Two-Electron System
Up: Identical Particles
Previous: Permutation Symmetry
Spin Statistics Theorem
We have seen that the exchange degeneracy of a system of identical particles is such that a specification of a complete set of
observable eigenvalues does not uniquely determine the corresponding state ket. However, we have also demonstrated that there are only two
possible state kets: that is, a ket that is totally symmetric with respect to particle interchange, or a ket that is totally antisymmetric.
It turns out that systems of identical particles possessing integer-spin (e.g., spin 0, or spin 1) always choose the totally symmetric
ket, whereas systems of identical particles possessing half-integer-spin (e.g., spin 1/2) always choose the totally antisymmetric ket.
This additional piece of information--which is generally known as the spin statistics theorem--ensures that the specification of a complete set of
observable eigenvalues of a system of identical particles does, in fact, uniquely determine the corresponding state ket.
Systems of identical particles whose state kets are totally symmetric with respect to particle interchange are said to
obey Bose-Einstein statistics [14,39]. Moreover, such particles are termed bosons. On the other hand,
systems of identical particles whose state kets are totally antisymmetric with respect to particle interchange are said to
obey Fermi-Dirac statistics [43,28], and the constituent particles are called fermions. In non-relativistic quantum mechanics, the rule that all integer-spin particles are bosons, whereas all half-integer spin
particles are fermions, must be accepted as an empirical fact. However, in relativistic quantum mechanics, it is possible
to formulate reasonably convincing arguments that half-integer-spin particles cannot be bosons, and integer-spin particles cannot be fermions [47,81].
Incidentally, electrons, protons, and neutrons are all fermions.
The Pauli exclusion principle [79] is an immediate consequence of the fact that electrons obey Fermi-Dirac statistics. This principle
states that no two electrons in a multi-electron system can possess identical sets of observable eigenvalues. For instance,
in the case of a three-electron system, the state ket is
[See Equation (9.41).]
Note, however, that
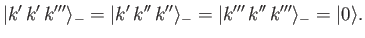 |
(9.43) |
In other words, if two of the electrons in the system possess the same set of observable eigenvalues then the state ket becomes the null ket, which corresponds to
the absence of a state.



Next: Two-Electron System
Up: Identical Particles
Previous: Permutation Symmetry
Richard Fitzpatrick
2016-01-22