Resonant Layers
Consider the situation, studied in the
previous section, in which a plane wave, polarized in the  -direction,
is launched along the
-direction,
is launched along the  -axis, from an antenna located at large positive
-axis, from an antenna located at large positive  ,
and absorbed at a resonance located at
,
and absorbed at a resonance located at 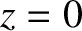 . In the vicinity
of the resonant point, the electric component of the wave satisfies
. In the vicinity
of the resonant point, the electric component of the wave satisfies
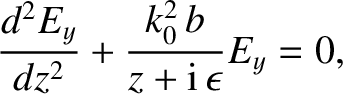 |
(6.55) |
where 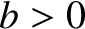 and
and
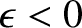 .
.
The time-averaged Poynting flux in the  -direction is written
-direction is written
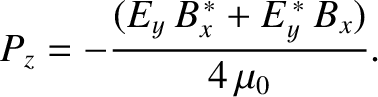 |
(6.56) |
Now, the Faraday-Maxwell equation yields
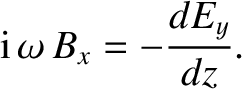 |
(6.57) |
Thus, we have
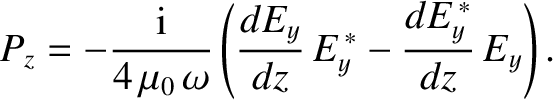 |
(6.58) |
Let us ascribe any variation of 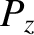 with
with  to the wave energy emitted by the
plasma. We then obtain
to the wave energy emitted by the
plasma. We then obtain
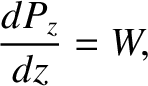 |
(6.59) |
where 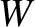 is the power emitted by the plasma per unit volume.
It follows that
is the power emitted by the plasma per unit volume.
It follows that
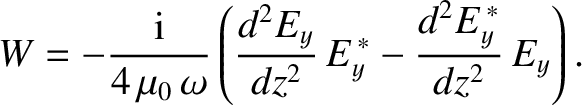 |
(6.60) |
Equations (6.55) and (6.60) yield
 |
(6.61) |
Note that  , because
, because
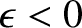 , so wave energy is absorbed by the
plasma. It is clear, from the previous formula, that the absorption takes
place in a narrow layer, of thickness
, so wave energy is absorbed by the
plasma. It is clear, from the previous formula, that the absorption takes
place in a narrow layer, of thickness
 , centered on the
resonance point,
, centered on the
resonance point, 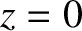 .
.
 -direction,
is launched along the
-direction,
is launched along the  -axis, from an antenna located at large positive
-axis, from an antenna located at large positive  ,
and absorbed at a resonance located at
,
and absorbed at a resonance located at 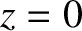 . In the vicinity
of the resonant point, the electric component of the wave satisfies
where
. In the vicinity
of the resonant point, the electric component of the wave satisfies
where 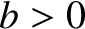 and
and
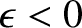 .
.
 -direction is written
-direction is written
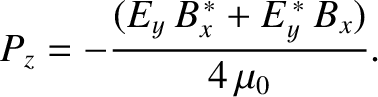
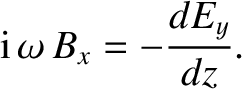
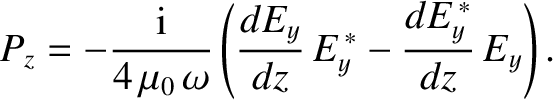
 with
with  to the wave energy emitted by the
plasma. We then obtain
to the wave energy emitted by the
plasma. We then obtain
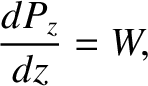
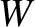 is the power emitted by the plasma per unit volume.
It follows that
Equations (6.55) and (6.60) yield
is the power emitted by the plasma per unit volume.
It follows that
Equations (6.55) and (6.60) yield

 , because
, because
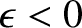 , so wave energy is absorbed by the
plasma. It is clear, from the previous formula, that the absorption takes
place in a narrow layer, of thickness
, so wave energy is absorbed by the
plasma. It is clear, from the previous formula, that the absorption takes
place in a narrow layer, of thickness
 , centered on the
resonance point,
, centered on the
resonance point, 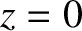 .
.