Next: Collisions Up: Plasma Parameters Previous: Debye Shielding Contents
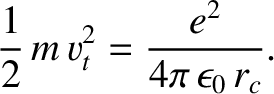 |
(1.18) |
The significance of the ratio 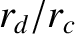 is readily understood. If this
ratio is small then charged particles are dominated by one another's electrostatic
influence more or less continuously, and their kinetic energies are small
compared to the interaction potential energies. Such plasmas are termed
strongly coupled. On the other hand, if the ratio is large then
strong electrostatic interactions between individual particles are
occasional, and relatively rare, events. A typical particle
is electrostatically influenced by all of the other particles within its
Debye sphere, but this interaction very rarely causes any sudden change in its motion.
Such plasmas are termed weakly coupled. It is possible to
describe a weakly coupled plasma using a modified Boltzmann equation
(in other words, the same type of equation that is conventionally used to describe a
neutral gas). (See Chapter 3.)
Understanding the strongly coupled limit is far more difficult, and will not
be attempted in this book. (Interested readers are directed to Fortov, Iakubov, and Khrapak 2007.) Actually, a strongly coupled plasma has more in
common with a liquid than a conventional weakly coupled plasma.
is readily understood. If this
ratio is small then charged particles are dominated by one another's electrostatic
influence more or less continuously, and their kinetic energies are small
compared to the interaction potential energies. Such plasmas are termed
strongly coupled. On the other hand, if the ratio is large then
strong electrostatic interactions between individual particles are
occasional, and relatively rare, events. A typical particle
is electrostatically influenced by all of the other particles within its
Debye sphere, but this interaction very rarely causes any sudden change in its motion.
Such plasmas are termed weakly coupled. It is possible to
describe a weakly coupled plasma using a modified Boltzmann equation
(in other words, the same type of equation that is conventionally used to describe a
neutral gas). (See Chapter 3.)
Understanding the strongly coupled limit is far more difficult, and will not
be attempted in this book. (Interested readers are directed to Fortov, Iakubov, and Khrapak 2007.) Actually, a strongly coupled plasma has more in
common with a liquid than a conventional weakly coupled plasma.
Let us define the plasma parameter,
This dimensionless parameter is obviously equal to the typical number of particles contained in a Debye sphere. However, Equations (1.8), (1.16), (1.17), and (1.19) can be combined to give It can be seen that the case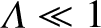 , in which the Debye
sphere is sparsely populated, corresponds to a strongly coupled plasma.
Likewise, the case
, in which the Debye
sphere is sparsely populated, corresponds to a strongly coupled plasma.
Likewise, the case
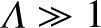 , in which the Debye sphere is
densely populated, corresponds to a weakly coupled plasma. It can also
be appreciated, from Equation (1.20), that strongly coupled plasmas
tend to be cold and dense, whereas weakly coupled plasmas tend to be diffuse and
hot. Examples of strongly coupled plasmas include solid density laser ablation
plasmas, the very “cold” (i.e., with kinetic temperatures
similar to the ionization energy) plasmas found in “high pressure” arc discharges, and the plasmas that constitute the
atmospheres of collapsed objects such as white dwarfs and neutron stars.
On the other hand, the hot diffuse plasmas typically encountered in ionospheric
physics, astrophysics, nuclear fusion, and space plasma physics are invariably
weakly coupled. Table 1.1 lists the key parameters for some typical
weakly coupled plasmas.
In conclusion, characteristic
plasma behavior is only observed on timescales
longer than the plasma period, and on lengthscales larger than the Debye length.
The statistical character of this behavior is controlled by the plasma parameter.
Although
, in which the Debye sphere is
densely populated, corresponds to a weakly coupled plasma. It can also
be appreciated, from Equation (1.20), that strongly coupled plasmas
tend to be cold and dense, whereas weakly coupled plasmas tend to be diffuse and
hot. Examples of strongly coupled plasmas include solid density laser ablation
plasmas, the very “cold” (i.e., with kinetic temperatures
similar to the ionization energy) plasmas found in “high pressure” arc discharges, and the plasmas that constitute the
atmospheres of collapsed objects such as white dwarfs and neutron stars.
On the other hand, the hot diffuse plasmas typically encountered in ionospheric
physics, astrophysics, nuclear fusion, and space plasma physics are invariably
weakly coupled. Table 1.1 lists the key parameters for some typical
weakly coupled plasmas.
In conclusion, characteristic
plasma behavior is only observed on timescales
longer than the plasma period, and on lengthscales larger than the Debye length.
The statistical character of this behavior is controlled by the plasma parameter.
Although 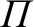 ,
,  , and
, and
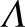 are the three most fundamental
plasma parameters, there are a number of other parameters that are worth
mentioning.
are the three most fundamental
plasma parameters, there are a number of other parameters that are worth
mentioning.