Debye Shielding
Plasmas generally do not contain strong electric fields in their
rest frames. The shielding of an external electric field from the
interior of a plasma can be viewed as a result of high plasma conductivity.
According to this explanation, electrical current can generally flow freely enough through a plasma to short out any interior electric fields.
However, it is more useful to consider the shielding as a dielectric
phenomenon. According to this explanation, it is the polarization of the plasma medium, and the
associated redistribution of space charge, that prevents penetration by an
external electric field. Not surprisingly, the lengthscale associated with such
shielding is the Debye length.
Let us consider the simplest possible example. Suppose that a quasi-neutral
plasma is sufficiently close to thermal equilibrium that the number densities of its two species
are distributed according to the Maxwell-Boltzmann law (Reif 1965),
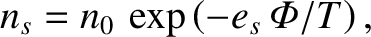 |
(1.11) |
where
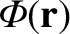 is the electrostatic potential, and
is the electrostatic potential, and 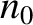 and
and
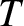 are constant. From
are constant. From
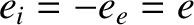 , it is clear that quasi-neutrality
requires the equilibrium potential to be zero. Suppose that the
equilibrium potential is perturbed, by an amount
, it is clear that quasi-neutrality
requires the equilibrium potential to be zero. Suppose that the
equilibrium potential is perturbed, by an amount
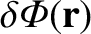 ,
as a consequence of a small, localized, perturbing charge density,
,
as a consequence of a small, localized, perturbing charge density,
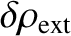 . The total
perturbed charge density is written
. The total
perturbed charge density is written
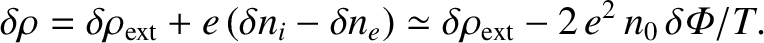 |
(1.12) |
Thus, Poisson's equation yields
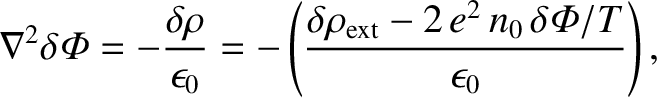 |
(1.13) |
which reduces to
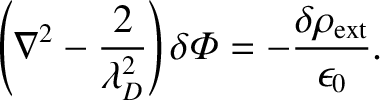 |
(1.14) |
If the perturbing charge density actually consists of a point charge 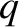 , located
at the origin, so that
, located
at the origin, so that
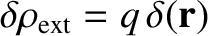 , then
the solution to the previous equation is written
, then
the solution to the previous equation is written
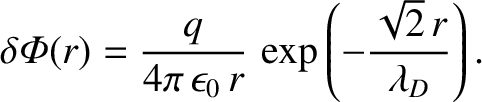 |
(1.15) |
This expression implies that the Coulomb potential of the perturbing point charge 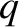 is
shielded over distances longer than the Debye length by a shielding
cloud of approximate radius
is
shielded over distances longer than the Debye length by a shielding
cloud of approximate radius 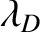 that consists of charge of the opposite sign.
that consists of charge of the opposite sign.
By treating 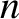 as a continuous function, the previous analysis implicitly
assumes that there are many particles in the shielding cloud. Actually,
Debye shielding remains statistically significant, and physical, in the
opposite limit in which the cloud is barely populated. In the latter case,
it is the
probability of observing charged particles within a Debye length of the
perturbing charge that is modified (Hazeltine and Waelbroeck 2004).
as a continuous function, the previous analysis implicitly
assumes that there are many particles in the shielding cloud. Actually,
Debye shielding remains statistically significant, and physical, in the
opposite limit in which the cloud is barely populated. In the latter case,
it is the
probability of observing charged particles within a Debye length of the
perturbing charge that is modified (Hazeltine and Waelbroeck 2004).
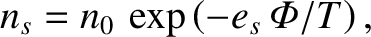
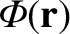 is the electrostatic potential, and
is the electrostatic potential, and 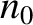 and
and
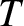 are constant. From
are constant. From
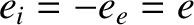 , it is clear that quasi-neutrality
requires the equilibrium potential to be zero. Suppose that the
equilibrium potential is perturbed, by an amount
, it is clear that quasi-neutrality
requires the equilibrium potential to be zero. Suppose that the
equilibrium potential is perturbed, by an amount
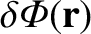 ,
as a consequence of a small, localized, perturbing charge density,
,
as a consequence of a small, localized, perturbing charge density,
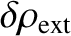 . The total
perturbed charge density is written
. The total
perturbed charge density is written
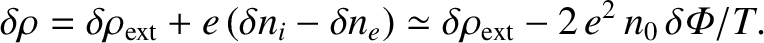
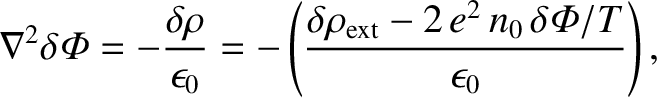
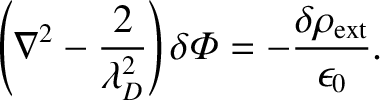
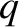 , located
at the origin, so that
, located
at the origin, so that
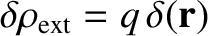 , then
the solution to the previous equation is written
, then
the solution to the previous equation is written
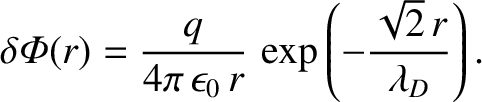
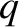 is
shielded over distances longer than the Debye length by a shielding
cloud of approximate radius
is
shielded over distances longer than the Debye length by a shielding
cloud of approximate radius 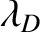 that consists of charge of the opposite sign.
that consists of charge of the opposite sign.
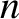 as a continuous function, the previous analysis implicitly
assumes that there are many particles in the shielding cloud. Actually,
Debye shielding remains statistically significant, and physical, in the
opposite limit in which the cloud is barely populated. In the latter case,
it is the
probability of observing charged particles within a Debye length of the
perturbing charge that is modified (Hazeltine and Waelbroeck 2004).
as a continuous function, the previous analysis implicitly
assumes that there are many particles in the shielding cloud. Actually,
Debye shielding remains statistically significant, and physical, in the
opposite limit in which the cloud is barely populated. In the latter case,
it is the
probability of observing charged particles within a Debye length of the
perturbing charge that is modified (Hazeltine and Waelbroeck 2004).