Next: Fluid Closure Up: Plasma Fluid Theory Previous: Fluid Equations Contents
 energy evolution equation, Equation (4.49), as
an entropy evolution equation (Hazeltine and Waelbroeck 2004). The fluid definition of entropy
density, which coincides with the thermodynamic entropy density in the
limit that the distribution function approaches a Maxwellian, is (Reif 1965)
where
energy evolution equation, Equation (4.49), as
an entropy evolution equation (Hazeltine and Waelbroeck 2004). The fluid definition of entropy
density, which coincides with the thermodynamic entropy density in the
limit that the distribution function approaches a Maxwellian, is (Reif 1965)
where 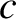 is a constant.
The corresponding entropy flux density is written
is a constant.
The corresponding entropy flux density is written
 |
(4.52) |
 |
(4.54) |
 can be regarded as the entropy production rate
per unit volume for species
can be regarded as the entropy production rate
per unit volume for species  . Evidently, entropy is produced by
collisional heating, viscous heating, and heat flow down temperature
gradients.
. Evidently, entropy is produced by
collisional heating, viscous heating, and heat flow down temperature
gradients.