It is conventional to rewrite our fluid equations in terms of the pressure tensor,
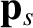 ,
the heat flux density,
,
the heat flux density,  , and the collisional heating rate in the local rest frame,
, and the collisional heating rate in the local rest frame, 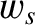 . Substituting from Equations (4.17), (4.18), and (4.30), and performing a little
tensor
algebra, Equations (4.36)–(4.38) reduce to:
Here,
. Substituting from Equations (4.17), (4.18), and (4.30), and performing a little
tensor
algebra, Equations (4.36)–(4.38) reduce to:
Here,
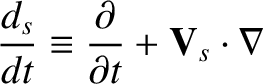 |
(4.44) |
is the well-known convective derivative, and
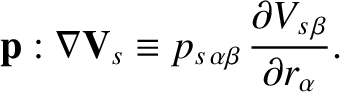 |
(4.45) |
In the previous expression, 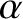 and
and 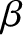 refer to Cartesian components, and repeated
indices are summed (in accordance with the Einstein summation convention) (Riley 1974).
The convective derivative, of course, measures time variation in
the local rest frame of the species-
refer to Cartesian components, and repeated
indices are summed (in accordance with the Einstein summation convention) (Riley 1974).
The convective derivative, of course, measures time variation in
the local rest frame of the species- fluid.
fluid.
There is one additional refinement to our fluid equations that is worth
carrying out. We introduce the generalized viscosity tensor,
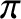
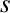 ,
by writing
,
by writing
where 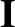 is the unit (identity) tensor. We expect the scalar
pressure term to dominate if the plasma is relatively close to thermal
equilibrium. We also expect, by analogy with conventional fluid theory, the
second term to describe viscous stresses. Indeed, this is generally the case
in plasmas,
although the generalized viscosity tensor can also include terms that are
quite unrelated to conventional viscosity. Equations (4.41)–(4.43) can, thus, be rewritten:
According to Equation (4.47), the species-
is the unit (identity) tensor. We expect the scalar
pressure term to dominate if the plasma is relatively close to thermal
equilibrium. We also expect, by analogy with conventional fluid theory, the
second term to describe viscous stresses. Indeed, this is generally the case
in plasmas,
although the generalized viscosity tensor can also include terms that are
quite unrelated to conventional viscosity. Equations (4.41)–(4.43) can, thus, be rewritten:
According to Equation (4.47), the species- density is constant along a fluid
trajectory unless the species-
density is constant along a fluid
trajectory unless the species- flow is non-solenoidal. For this reason,
the condition
flow is non-solenoidal. For this reason,
the condition
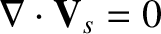 |
(4.50) |
is said to describe incompressible species- flow. According to
Equation (4.48), the species-
flow. According to
Equation (4.48), the species- flow accelerates
along a fluid trajectory under the influence of the
scalar pressure gradient, the viscous stresses, the Lorentz force, and the
frictional force due to collisions with other species. Finally,
according to Equation (4.49), the species-
flow accelerates
along a fluid trajectory under the influence of the
scalar pressure gradient, the viscous stresses, the Lorentz force, and the
frictional force due to collisions with other species. Finally,
according to Equation (4.49), the species- energy density (that is,
energy density (that is, 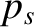 )
changes along a fluid trajectory
because of the work done in compressing the fluid, viscous heating,
heat flow, and the local energy gain due to collisions with other species.
The electrical contribution to plasma heating, which was explicit
in Equation (4.38), has now become entirely implicit.
)
changes along a fluid trajectory
because of the work done in compressing the fluid, viscous heating,
heat flow, and the local energy gain due to collisions with other species.
The electrical contribution to plasma heating, which was explicit
in Equation (4.38), has now become entirely implicit.
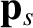 ,
the heat flux density,
,
the heat flux density,  , and the collisional heating rate in the local rest frame,
, and the collisional heating rate in the local rest frame, 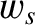 . Substituting from Equations (4.17), (4.18), and (4.30), and performing a little
tensor
algebra, Equations (4.36)–(4.38) reduce to:
Here,
. Substituting from Equations (4.17), (4.18), and (4.30), and performing a little
tensor
algebra, Equations (4.36)–(4.38) reduce to:
Here,
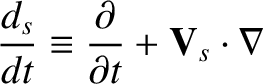
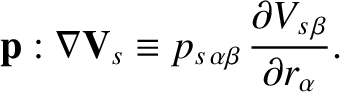
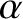 and
and 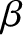 refer to Cartesian components, and repeated
indices are summed (in accordance with the Einstein summation convention) (Riley 1974).
The convective derivative, of course, measures time variation in
the local rest frame of the species-
refer to Cartesian components, and repeated
indices are summed (in accordance with the Einstein summation convention) (Riley 1974).
The convective derivative, of course, measures time variation in
the local rest frame of the species- fluid.
fluid.
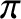
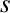 ,
by writing
,
by writing
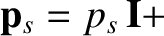
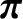
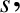
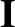 is the unit (identity) tensor. We expect the scalar
pressure term to dominate if the plasma is relatively close to thermal
equilibrium. We also expect, by analogy with conventional fluid theory, the
second term to describe viscous stresses. Indeed, this is generally the case
in plasmas,
although the generalized viscosity tensor can also include terms that are
quite unrelated to conventional viscosity. Equations (4.41)–(4.43) can, thus, be rewritten:
According to Equation (4.47), the species-
is the unit (identity) tensor. We expect the scalar
pressure term to dominate if the plasma is relatively close to thermal
equilibrium. We also expect, by analogy with conventional fluid theory, the
second term to describe viscous stresses. Indeed, this is generally the case
in plasmas,
although the generalized viscosity tensor can also include terms that are
quite unrelated to conventional viscosity. Equations (4.41)–(4.43) can, thus, be rewritten:
According to Equation (4.47), the species- density is constant along a fluid
trajectory unless the species-
density is constant along a fluid
trajectory unless the species- flow is non-solenoidal. For this reason,
the condition
flow is non-solenoidal. For this reason,
the condition
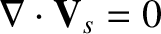
 flow. According to
Equation (4.48), the species-
flow. According to
Equation (4.48), the species- flow accelerates
along a fluid trajectory under the influence of the
scalar pressure gradient, the viscous stresses, the Lorentz force, and the
frictional force due to collisions with other species. Finally,
according to Equation (4.49), the species-
flow accelerates
along a fluid trajectory under the influence of the
scalar pressure gradient, the viscous stresses, the Lorentz force, and the
frictional force due to collisions with other species. Finally,
according to Equation (4.49), the species- energy density (that is,
energy density (that is, 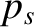 )
changes along a fluid trajectory
because of the work done in compressing the fluid, viscous heating,
heat flow, and the local energy gain due to collisions with other species.
The electrical contribution to plasma heating, which was explicit
in Equation (4.38), has now become entirely implicit.
)
changes along a fluid trajectory
because of the work done in compressing the fluid, viscous heating,
heat flow, and the local energy gain due to collisions with other species.
The electrical contribution to plasma heating, which was explicit
in Equation (4.38), has now become entirely implicit.