An adiabatic invariant is an approximation to a more fundamental type of
invariant known as a Poincaré invariant (Hazeltine and Waelbroeck 2004). A Poincaré invariant
takes the form
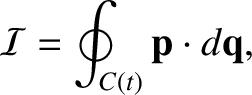 |
(2.71) |
where all points on the closed curve 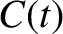 in phase-space move
according to the equations of motion.
in phase-space move
according to the equations of motion.
In order to demonstrate that  is a constant of the motion, we
introduce a periodic variable
is a constant of the motion, we
introduce a periodic variable  parameterizing the points on the curve
parameterizing the points on the curve  .
The coordinates of a general point on
.
The coordinates of a general point on  are thus written
are thus written
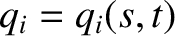 and
and
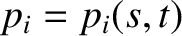 . The rate of change of
. The rate of change of  is then
is then
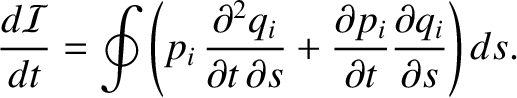 |
(2.72) |
Let us integrate the first term by parts, and then use Hamilton's
equations of motion to simplify the result (Goldstein, Poole, and Safko 2002). We obtain
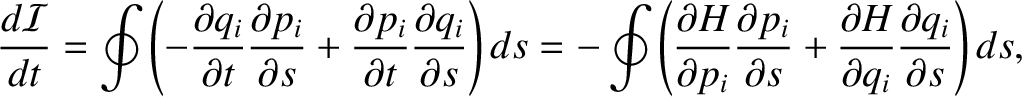 |
(2.73) |
where
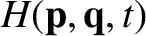 is the Hamiltonian for the motion.
The integrand is now seen to be the total derivative of
is the Hamiltonian for the motion.
The integrand is now seen to be the total derivative of 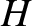 along
along  .
Because the Hamiltonian is a single-valued function, it follows that
.
Because the Hamiltonian is a single-valued function, it follows that
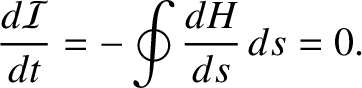 |
(2.74) |
Thus,  is indeed a constant of the motion.
is indeed a constant of the motion.
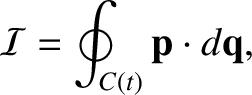
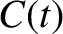 in phase-space move
according to the equations of motion.
in phase-space move
according to the equations of motion.
 is a constant of the motion, we
introduce a periodic variable
is a constant of the motion, we
introduce a periodic variable  parameterizing the points on the curve
parameterizing the points on the curve  .
The coordinates of a general point on
.
The coordinates of a general point on  are thus written
are thus written
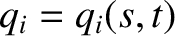 and
and
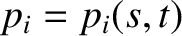 . The rate of change of
. The rate of change of  is then
is then
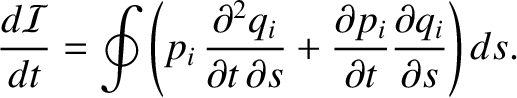
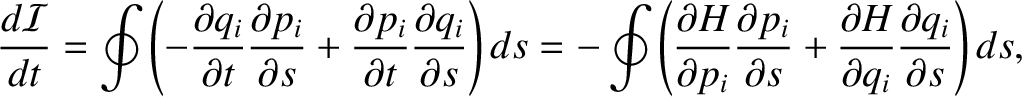
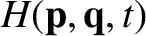 is the Hamiltonian for the motion.
The integrand is now seen to be the total derivative of
is the Hamiltonian for the motion.
The integrand is now seen to be the total derivative of 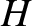 along
along  .
Because the Hamiltonian is a single-valued function, it follows that
.
Because the Hamiltonian is a single-valued function, it follows that
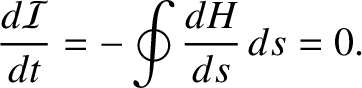
 is indeed a constant of the motion.
is indeed a constant of the motion.