Invariance of Magnetic Moment
Let us now demonstrate that the magnetic moment,
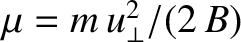 ,
is indeed a constant of the motion, at least to lowest order. The scalar
product of the equation of motion, Equation (2.24), with the velocity
,
is indeed a constant of the motion, at least to lowest order. The scalar
product of the equation of motion, Equation (2.24), with the velocity 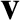 yields
yields
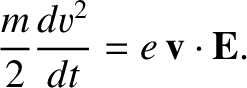 |
(2.60) |
This equation governs the evolution of the particle energy during its
motion. Let us make the substitution
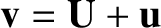 ,
as before, and then average the preceding equation over gyrophase. To lowest order, we obtain
Here, use has been made of the result
,
as before, and then average the preceding equation over gyrophase. To lowest order, we obtain
Here, use has been made of the result
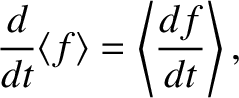 |
(2.62) |
which is valid for any 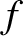 . The final term on the right-hand side of
Equation (2.61) can be written
where use has been made of Equation (2.44).
Thus, Equation (2.61) reduces to
Here,
. The final term on the right-hand side of
Equation (2.61) can be written
where use has been made of Equation (2.44).
Thus, Equation (2.61) reduces to
Here, 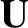 is the guiding center velocity, evaluated to first order, and
is the guiding center velocity, evaluated to first order, and
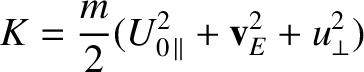 |
(2.65) |
is the lowest order kinetic energy of the particle. Evidently, the kinetic energy can
change in one of two different ways. First, by motion of the guiding center along the
direction of the electric field, and, second, by acceleration of the gyration due
to the electromotive force generated around the Larmor orbit by a
changing magnetic field.
Equation (2.64) yields
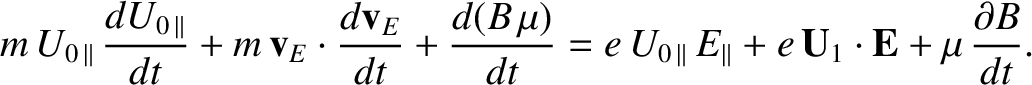 |
(2.66) |
It follows from Equation (2.50) that
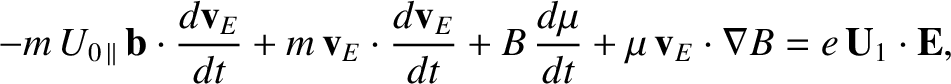 |
(2.67) |
where use has been made of
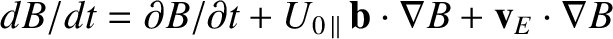 .
However,
.
However,
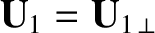 . Moreover, according to Equations (2.4), (2.35), and (2.51),
. Moreover, according to Equations (2.4), (2.35), and (2.51),
![$\displaystyle e\,{\bf U}_1\cdot{\bf E} = m\,{\bf v}_E\cdot\left[\frac{d}{dt}\,(U_{0\,\parallel}\,{\bf b} + {\bf v}_E) + \frac{\mu}{m}\,\nabla B\right].$](img381.png) |
(2.68) |
Hence, Equation (2.67) reduces to
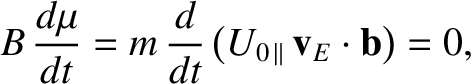 |
(2.69) |
which implies that
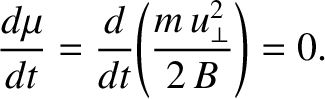 |
(2.70) |
Thus, to lowest order, the magnetic moment, 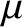 , is a constant of the motion.
Kruskal has shown that
, is a constant of the motion.
Kruskal has shown that
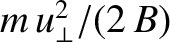 is, in fact, the lowest order
approximation to a quantity that is a constant of the motion to
all orders in the perturbation expansion (Kruskal 1962). Such a quantity
is termed an adiabatic invariant.
is, in fact, the lowest order
approximation to a quantity that is a constant of the motion to
all orders in the perturbation expansion (Kruskal 1962). Such a quantity
is termed an adiabatic invariant.
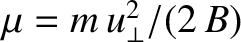 ,
is indeed a constant of the motion, at least to lowest order. The scalar
product of the equation of motion, Equation (2.24), with the velocity
,
is indeed a constant of the motion, at least to lowest order. The scalar
product of the equation of motion, Equation (2.24), with the velocity 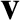 yields
yields
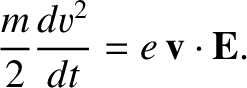
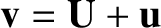 ,
as before, and then average the preceding equation over gyrophase. To lowest order, we obtain
Here, use has been made of the result
,
as before, and then average the preceding equation over gyrophase. To lowest order, we obtain
Here, use has been made of the result
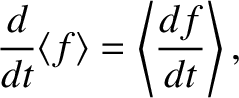
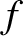 . The final term on the right-hand side of
Equation (2.61) can be written
. The final term on the right-hand side of
Equation (2.61) can be written
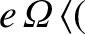
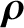
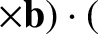
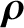
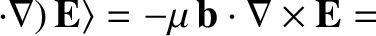
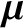
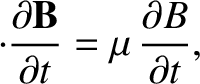
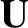 is the guiding center velocity, evaluated to first order, and
is the guiding center velocity, evaluated to first order, and
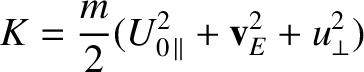
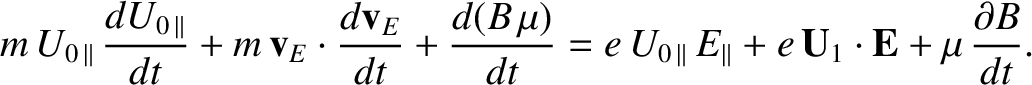
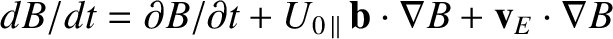 .
However,
.
However,
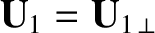 . Moreover, according to Equations (2.4), (2.35), and (2.51),
. Moreover, according to Equations (2.4), (2.35), and (2.51),
![$\displaystyle e\,{\bf U}_1\cdot{\bf E} = m\,{\bf v}_E\cdot\left[\frac{d}{dt}\,(U_{0\,\parallel}\,{\bf b} + {\bf v}_E) + \frac{\mu}{m}\,\nabla B\right].$](img381.png)
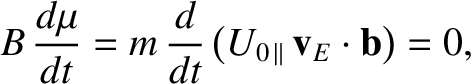
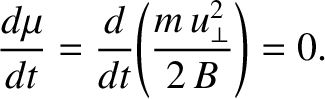
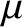 , is a constant of the motion.
Kruskal has shown that
, is a constant of the motion.
Kruskal has shown that
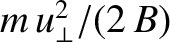 is, in fact, the lowest order
approximation to a quantity that is a constant of the motion to
all orders in the perturbation expansion (Kruskal 1962). Such a quantity
is termed an adiabatic invariant.
is, in fact, the lowest order
approximation to a quantity that is a constant of the motion to
all orders in the perturbation expansion (Kruskal 1962). Such a quantity
is termed an adiabatic invariant.