Next: Guiding Center Motion Up: Charged Particle Motion Previous: Motion in Uniform Fields Contents
Consider the equation of motion
where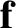 is a periodic function of its last argument, with
period
is a periodic function of its last argument, with
period  , and
Here, the small parameter
, and
Here, the small parameter  characterizes the separation between the
short oscillation period and the timescale for the slow secular evolution
of the “position”
characterizes the separation between the
short oscillation period and the timescale for the slow secular evolution
of the “position” 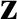 .
.
The basic idea of the averaging method is to treat 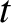 and
and 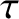 as distinct
independent variables, and to look for solutions of the form
as distinct
independent variables, and to look for solutions of the form
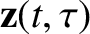 that are periodic in
that are periodic in 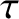 . Thus, we replace Equation (2.8) by
. Thus, we replace Equation (2.8) by
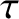 . All of the secular drifts
are thereby attributed to the variable
. All of the secular drifts
are thereby attributed to the variable 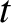 , while the oscillations are
described entirely by the variable
, while the oscillations are
described entirely by the variable 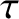 .
.
Let us denote the 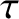 -average of
-average of 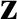 by
by 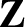 , and seek a
change of variables of the form
, and seek a
change of variables of the form
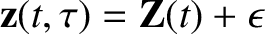  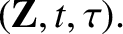 |
(2.11) |
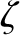 is a periodic function of
is a periodic function of 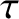 with vanishing mean.
Thus,
with vanishing mean.
Thus,
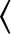  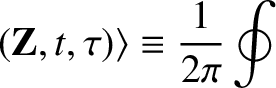  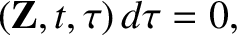 |
(2.12) |
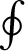 denotes the integral over a full period in
denotes the integral over a full period in 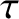 .
.
The evolution of 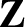 is determined by substituting the
expansions
is determined by substituting the
expansions
 |
  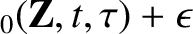     |
(2.13) |
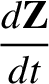 |
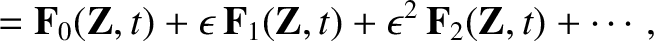 |
(2.14) |
 .
.
To lowest order, we obtain
The solubility condition for this equation is Integrating the oscillating component of Equation (2.15) yields ![$\displaystyle _0 ({\bf Z}, t,\tau) = \int_0^\tau\left[
{\bf f}({\bf Z},t,\tau') - \langle{\bf f}\rangle({\bf Z},t)\right]d\tau'.$](img262.png) |
(2.17) |
To first order, Equation (2.10) gives,
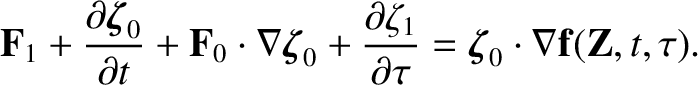 |
(2.18) |
The final result is obtained by combining Equations (2.14), (2.16), and (2.19):
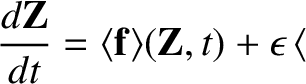  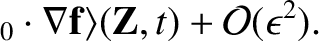 |
(2.20) |
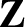 is determined to lowest order by the average of the “force”
is determined to lowest order by the average of the “force” 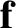 , and to
next order by the correlation between the oscillation in the “position”
, and to
next order by the correlation between the oscillation in the “position”
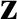 and the
oscillation in the spatial gradient of the “force.”
and the
oscillation in the spatial gradient of the “force.”