Moments of Collision Operator
The most important moments of the collision operator (see Section 4.3) are the friction force density,
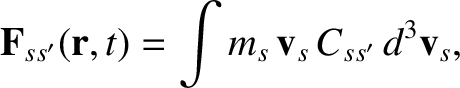 |
(3.163) |
acting on species- particles due to collisions with species-
particles due to collisions with species- particles, the
friction force density,
particles, the
friction force density,
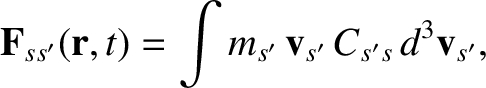 |
(3.164) |
acting on species- particles due to collisions with species-
particles due to collisions with species- particles,
the collisional heating rate density,
particles,
the collisional heating rate density,
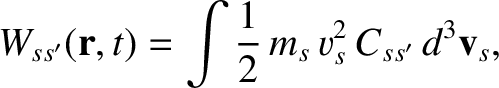 |
(3.165) |
experienced by species- particles due to collisions with species-
particles due to collisions with species- particles, and
the collisional heating rate density,
particles, and
the collisional heating rate density,
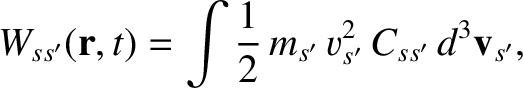 |
(3.166) |
experienced by species- particles due to collisions with species-
particles due to collisions with species- particles. However, as
is clear from Equations (3.35) and (3.37),
particles. However, as
is clear from Equations (3.35) and (3.37),
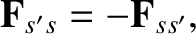 |
(3.167) |
and
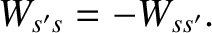 |
(3.168) |
Hence, we only need to determine
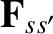 and
and 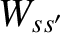 . Let us calculate these quantities using the Maxwellian collision operator (3.163).
. Let us calculate these quantities using the Maxwellian collision operator (3.163).
Equations (3.163) and (3.164) imply that
where we have integrated by parts.
However, it follows from symmetry that
where 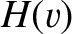 is a general function. Hence, we obtain
is a general function. Hence, we obtain
![$\displaystyle F_{ss'\,\alpha} =-\frac{2\,\gamma_{ss'}\,n_s\,n_{s'}\,V_{s\,\alph...
...{v\,v_{t\,s}^{2}}-\frac{T_{s'}}{T_s}\,\frac{F_{2}-F_1}{v^{3}}\right]d^3{\bf v},$](img943.png) |
(3.173) |
which yields
![$\displaystyle F_{ss'\,\alpha} =-\frac{16\,\gamma_{ss'}\,n_s\,n_{s'}\,V_{s\,\alp...
...ght)\zeta\,F_1(\zeta)+\frac{T_{s'}}{T_s}\,\zeta\,{\rm erf}(\zeta)\right]d\zeta,$](img944.png) |
(3.174) |
where
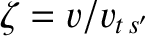 and
and
 . It is easily demonstrated that (Abramowitz and Stegun 1965)
Thus, we get
. It is easily demonstrated that (Abramowitz and Stegun 1965)
Thus, we get
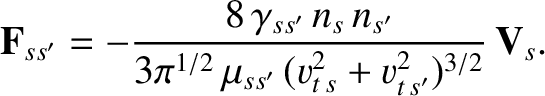 |
(3.177) |
Suppose that we transform to a new frame of reference that moves with velocity  with respect to our original
frame. In the new reference frame,
with respect to our original
frame. In the new reference frame,
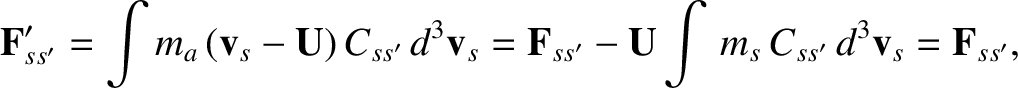 |
(3.178) |
where use has been made of the collisional conservation law (3.31). It follows that
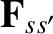 is invariant under Galilean
transformations. This implies that the quantity
is invariant under Galilean
transformations. This implies that the quantity 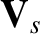 , appearing in Equation (3.178), must be reinterpreted as the relative mean flow velocity,
, appearing in Equation (3.178), must be reinterpreted as the relative mean flow velocity,
 , between species-
, between species- and species-
and species- particles.
Of course,
particles.
Of course,
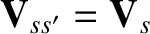 in our adopted reference frame in which
in our adopted reference frame in which
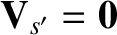 . It follows that the general expression for the
friction force density is
. It follows that the general expression for the
friction force density is
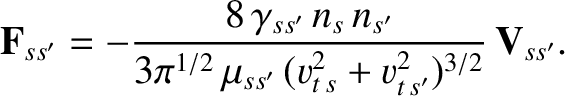 |
(3.179) |
Note that this expression satisfies the collisional momentum conservation constraint (3.168). Furthermore, it is clear that the collisional
friction force acts to reduce the relative mean flow velocity,
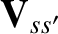 , of species-
, of species- and species-
and species- particles.
Note that
particles.
Note that
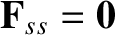 . In other words, a plasma species cannot exert a frictional force on itself.
. In other words, a plasma species cannot exert a frictional force on itself.
Equations (3.163) and (3.166) imply that
where we have integrated by parts. Making use of Equation (3.171)–(3.173), the previous expression reduces to
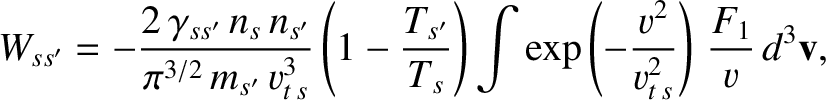 |
(3.181) |
which gives
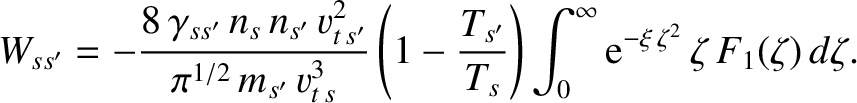 |
(3.182) |
It follows from Equation (3.176) that
 |
(3.183) |
Note that this expression satisfies the collisional energy conservation constraint (3.169). Furthermore, it is clear that the collisional
heating acts to reduce the temperature difference of species- and species-
and species- particles. Note that
particles. Note that 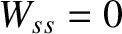 . In other words, a plasma species cannot heat itself by means of collisions.
. In other words, a plasma species cannot heat itself by means of collisions.
 particles due to collisions with species-
particles due to collisions with species- particles, the
friction force density,
particles, the
friction force density,
 particles due to collisions with species-
particles due to collisions with species- particles,
the collisional heating rate density,
experienced by species-
particles,
the collisional heating rate density,
experienced by species- particles due to collisions with species-
particles due to collisions with species- particles, and
the collisional heating rate density,
particles, and
the collisional heating rate density,
 particles due to collisions with species-
particles due to collisions with species- particles. However, as
is clear from Equations (3.35) and (3.37),
and
Hence, we only need to determine
particles. However, as
is clear from Equations (3.35) and (3.37),
and
Hence, we only need to determine
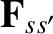 and
and 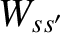 . Let us calculate these quantities using the Maxwellian collision operator (3.163).
. Let us calculate these quantities using the Maxwellian collision operator (3.163).
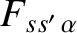

![$\displaystyle \phantom{=}\left.-\frac{T_{s'}}{T_s}\,\frac{V_{s\,\beta}}{v^{3}}\...
...pha\beta}-(F_2+2\,F_1)\frac{v_\alpha\,v_\beta}{v^{2}}\right]\right\}d^3{\bf v},$](img937.png)
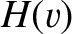 is a general function. Hence, we obtain
is a general function. Hence, we obtain
![$\displaystyle F_{ss'\,\alpha} =-\frac{2\,\gamma_{ss'}\,n_s\,n_{s'}\,V_{s\,\alph...
...{v\,v_{t\,s}^{2}}-\frac{T_{s'}}{T_s}\,\frac{F_{2}-F_1}{v^{3}}\right]d^3{\bf v},$](img943.png)
![$\displaystyle F_{ss'\,\alpha} =-\frac{16\,\gamma_{ss'}\,n_s\,n_{s'}\,V_{s\,\alp...
...ght)\zeta\,F_1(\zeta)+\frac{T_{s'}}{T_s}\,\zeta\,{\rm erf}(\zeta)\right]d\zeta,$](img944.png)
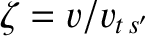 and
and
 . It is easily demonstrated that (Abramowitz and Stegun 1965)
. It is easily demonstrated that (Abramowitz and Stegun 1965)
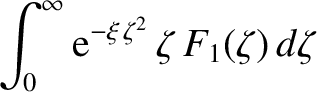
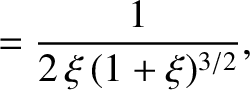
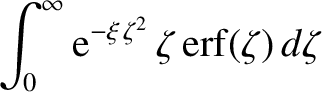
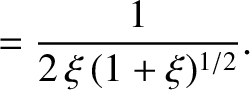
 with respect to our original
frame. In the new reference frame,
with respect to our original
frame. In the new reference frame,
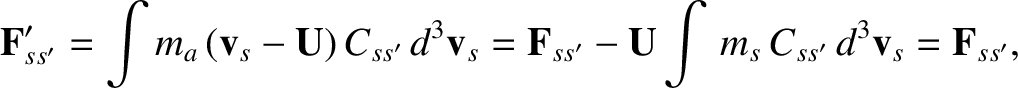
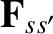 is invariant under Galilean
transformations. This implies that the quantity
is invariant under Galilean
transformations. This implies that the quantity 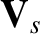 , appearing in Equation (3.178), must be reinterpreted as the relative mean flow velocity,
, appearing in Equation (3.178), must be reinterpreted as the relative mean flow velocity,
 , between species-
, between species- and species-
and species- particles.
Of course,
particles.
Of course,
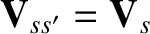 in our adopted reference frame in which
in our adopted reference frame in which
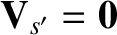 . It follows that the general expression for the
friction force density is
Note that this expression satisfies the collisional momentum conservation constraint (3.168). Furthermore, it is clear that the collisional
friction force acts to reduce the relative mean flow velocity,
. It follows that the general expression for the
friction force density is
Note that this expression satisfies the collisional momentum conservation constraint (3.168). Furthermore, it is clear that the collisional
friction force acts to reduce the relative mean flow velocity,
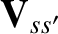 , of species-
, of species- and species-
and species- particles.
Note that
particles.
Note that
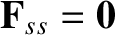 . In other words, a plasma species cannot exert a frictional force on itself.
. In other words, a plasma species cannot exert a frictional force on itself.
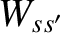
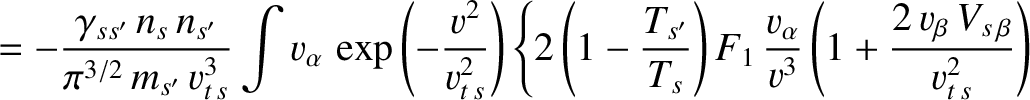
![$\displaystyle \phantom{=}\left.-\frac{T_{s'}}{T_s}\,\frac{V_{s\,\beta}}{v^{3}}\...
...a\beta}-(F_{2}+2\,F_1)\frac{v_\alpha\,v_\beta}{v^{2}}\right]\right\}d^3{\bf v},$](img960.png)
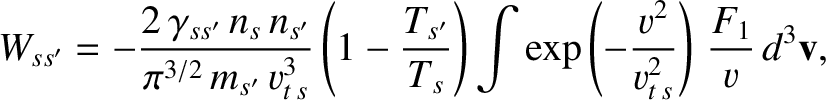
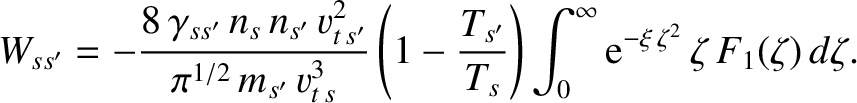
 and species-
and species- particles. Note that
particles. Note that 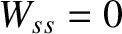 . In other words, a plasma species cannot heat itself by means of collisions.
. In other words, a plasma species cannot heat itself by means of collisions.