


Next: Rosenbluth Potentials
Up: Collisions
Previous: Landau Collision Operator
Coulomb Logarithm
According to Equation (3.103), the Coulomb logarithm can be written
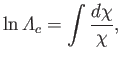 |
(3.117) |
where we have made use of the fact that scattering angle 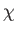 is small,
Obviously, the integral appearing in the previous expression diverges at both large and small
is small,
Obviously, the integral appearing in the previous expression diverges at both large and small 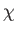 .
.
The divergence of the integral on the right-hand side of the previous equation at large 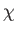 is a consequence of the breakdown of the small-angle approximation. The standard prescription
for avoiding this divergence is to truncate the integral at some
is a consequence of the breakdown of the small-angle approximation. The standard prescription
for avoiding this divergence is to truncate the integral at some
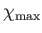 above which the small-angle approximation becomes
invalid. According to Equation (3.102), this truncation is equivalent to neglecting all collisions whose impact parameters
fall below the value
above which the small-angle approximation becomes
invalid. According to Equation (3.102), this truncation is equivalent to neglecting all collisions whose impact parameters
fall below the value
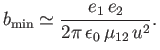 |
(3.118) |
The ultimate justification for the truncation of the integral appearing in Equation (3.117) at large 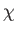 is the idea that Coulomb collisions are dominated by small-angle scattering events, and that
the occasional large-angle scattering events have a negligible effect on the scattering statistics. Unfortunately, this is not quite true (if it were then the integral would converge at large
is the idea that Coulomb collisions are dominated by small-angle scattering events, and that
the occasional large-angle scattering events have a negligible effect on the scattering statistics. Unfortunately, this is not quite true (if it were then the integral would converge at large 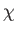 ). However, the
rare large-angle scattering events only make a relatively weak logarithmic contribution to the scattering statistics.
). However, the
rare large-angle scattering events only make a relatively weak logarithmic contribution to the scattering statistics.
Making the estimate
 , where
, where 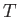 is the assumed common temperature of the
two colliding species, we obtain
is the assumed common temperature of the
two colliding species, we obtain
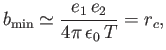 |
(3.119) |
where 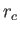 is the classical distance of closest approach introduced in Section 1.6.
However, as mentioned in Section 1.10, it is possible for the classical distance of closest approach
to fall below the de Broglie wavelength of one or both of the colliding particles, even in the case of a weakly coupled plasma.
In this situation, the most sensible thing to do is to approximate
is the classical distance of closest approach introduced in Section 1.6.
However, as mentioned in Section 1.10, it is possible for the classical distance of closest approach
to fall below the de Broglie wavelength of one or both of the colliding particles, even in the case of a weakly coupled plasma.
In this situation, the most sensible thing to do is to approximate
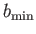 as the larger de Broglie wavelength (Spitzer 1956; Braginskii 1965).
as the larger de Broglie wavelength (Spitzer 1956; Braginskii 1965).
The divergence of the integral on the right-hand side of Equation (3.117) at small 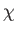 is a consequence of the
infinite range of the Coulomb potential. The standard prescription
for avoiding this divergence is to take the Debye shielding of the Coulomb potential into account. (See Section 1.5.) This is equivalent to
neglecting all collisions whose impact parameters exceed the value
is a consequence of the
infinite range of the Coulomb potential. The standard prescription
for avoiding this divergence is to take the Debye shielding of the Coulomb potential into account. (See Section 1.5.) This is equivalent to
neglecting all collisions whose impact parameters exceed the value
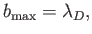 |
(3.120) |
where  is the Debye length. Of course, Debye shielding is a many-particle effect. Hence, the Landau collision operator can no longer be regarded as a
pure two-body collision operator. Fortunately, however, many-particle effects only make a relatively weak logarithmic contribution to the operator.
is the Debye length. Of course, Debye shielding is a many-particle effect. Hence, the Landau collision operator can no longer be regarded as a
pure two-body collision operator. Fortunately, however, many-particle effects only make a relatively weak logarithmic contribution to the operator.
According to Equations (3.104), (3.119), and (3.120),
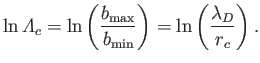 |
(3.121) |
Thus, we deduce from Equation (1.20) that
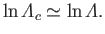 |
(3.122) |
In other words, the Coulomb logarithm is approximately equal to the natural logarithm of the plasma parameter.
The fact that the plasma parameter is much larger than unity in a weakly coupled plasma implies that the
Coulomb logarithm is large compared to unity in such a plasma. In fact,
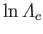 lies in the range
lies in the range
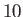 -
-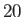 for typical weakly coupled plasmas. It also follows that
for typical weakly coupled plasmas. It also follows that
 in a
weakly coupled plasma, which means that there is a large range of impact parameters for which it is accurate to treat Coulomb collisions
as small-angle two-body scattering events.
in a
weakly coupled plasma, which means that there is a large range of impact parameters for which it is accurate to treat Coulomb collisions
as small-angle two-body scattering events.
The official definition of the Coulomb logarithm is as follows (Huba 2000d). For a particle of type  ,
with mass
,
with mass 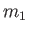 and charge
and charge
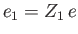 , scattered by particles of type
, scattered by particles of type  , with mass
, with mass 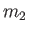 and charge
and charge
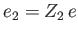 ,
the Coulomb logarithm is defined
,
the Coulomb logarithm is defined
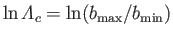 . Here,
. Here,
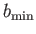 is the larger of
is the larger of
 and
and
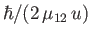 , averaged over both particle
distributions, where
, averaged over both particle
distributions, where
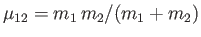 and
and
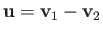 . Furthermore,
. Furthermore,
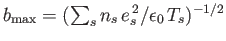 , where the
summation extends over all species,
, where the
summation extends over all species, 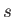 , for which
, for which
 .
For thermal (i.e., Maxwellian) electron-electron collisions, we obtain
.
For thermal (i.e., Maxwellian) electron-electron collisions, we obtain
Likewise, for thermal electron-ion collisions, we get
Here,  and
and 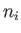 are measured in units of
are measured in units of
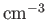 , whereas
, whereas 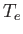 and
and  are measured in units of
electron-volts. Moreover,
are measured in units of
electron-volts. Moreover,
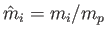 , where
, where 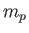 is the proton mass.
is the proton mass.
The standard approach in plasma physics is to treat the Coulomb logarithm as a constant, with a value determined by the ambient
electron number density, the ambient electron and ion temperatures, and the ion charge and mass numbers, as has just been described. This approximation ensures that the Landau collision
operator,
 , is strictly bilinear in its two arguments.
, is strictly bilinear in its two arguments.



Next: Rosenbluth Potentials
Up: Collisions
Previous: Landau Collision Operator
Richard Fitzpatrick
2016-01-23
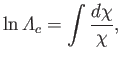
![]() is a consequence of the breakdown of the small-angle approximation. The standard prescription
for avoiding this divergence is to truncate the integral at some
is a consequence of the breakdown of the small-angle approximation. The standard prescription
for avoiding this divergence is to truncate the integral at some
![]() above which the small-angle approximation becomes
invalid. According to Equation (3.102), this truncation is equivalent to neglecting all collisions whose impact parameters
fall below the value
above which the small-angle approximation becomes
invalid. According to Equation (3.102), this truncation is equivalent to neglecting all collisions whose impact parameters
fall below the value
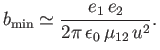
![]() , where
, where ![]() is the assumed common temperature of the
two colliding species, we obtain
is the assumed common temperature of the
two colliding species, we obtain
![]() is a consequence of the
infinite range of the Coulomb potential. The standard prescription
for avoiding this divergence is to take the Debye shielding of the Coulomb potential into account. (See Section 1.5.) This is equivalent to
neglecting all collisions whose impact parameters exceed the value
is a consequence of the
infinite range of the Coulomb potential. The standard prescription
for avoiding this divergence is to take the Debye shielding of the Coulomb potential into account. (See Section 1.5.) This is equivalent to
neglecting all collisions whose impact parameters exceed the value
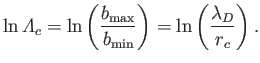
![]() ,
with mass
,
with mass ![]() and charge
and charge
![]() , scattered by particles of type
, scattered by particles of type ![]() , with mass
, with mass ![]() and charge
and charge
![]() ,
the Coulomb logarithm is defined
,
the Coulomb logarithm is defined
![]() . Here,
. Here,
![]() is the larger of
is the larger of
![]() and
and
![]() , averaged over both particle
distributions, where
, averaged over both particle
distributions, where
![]() and
and
![]() . Furthermore,
. Furthermore,
![]() , where the
summation extends over all species,
, where the
summation extends over all species, ![]() , for which
, for which
![]() .
For thermal (i.e., Maxwellian) electron-electron collisions, we obtain
.
For thermal (i.e., Maxwellian) electron-electron collisions, we obtain
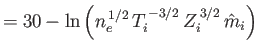
![]() , is strictly bilinear in its two arguments.
, is strictly bilinear in its two arguments.